Small semitone.
Ramsay
Comma - The ratio of 80:81 - not an interval, but a fraction of an interval. [Scientific Basis and Build of Music, page 25]
"While vibrations are the sound-stuff, the protoplasm of notes, semitones are, as it were, the atoms of which music is composed. We may think and talk of quarter tones and commas, apotomes and skismas, and dots, but these have no place as intervals for the musical ear, nor any part in the compositions which so charm us of the great masters." [Scientific Basis and Build of Music, page 20]
Getting Fifths as we ascend toward the number twelve they are in themselves the same, but with regard to their relationships they are quite different. Before and up to the twelfth fifth no scale has all the notes at the same distance above the first scale of the series. But after twelve, the thirteenth scale for example, B#, supposing the scale to be marked by sharps only, is a comma and a very small ratio above C; Cx is the same distance above D of the first scale; Dx the same above E; E# is the same distance above F; Fx the same distance above G; Gx the same distance above A; and Ax the same distance above B. So the scale of B# is just the scale of C over again at the distance of twelve-fifths, only it is a comma and the apotome minor higher; and each series of twelve-fifths is this distance higher than the preceding one. [Scientific Basis and Build of Music, page 30]
The extremes of the levities and gravities of a key-system are always at the extent of three fifths; and whatever notes are adopted for these three fifths, the center fifth is the tonic. As there never can be more than three fifths above each other on the same terms, so there can never be more than one such scale at the same time. A fourth fifth is a comma less than the harmonic fifth1; and this is Nature's danger-signal, to show that it is not admissible here. Nature does not sew with a knotless thread in music. The elements are so place that nothing can be added nor anything taken away without producing confusion or defect. What has been created is thus at the same time protected by Nature. [Scientific Basis and Build of Music, page 38]
The structure and quantity of the three fifths in a major scale are always 9, 8, 9, 5 = 31 commas; but the structure and quantity of the
fourth fifth is 8, 5, 9, 8 = 30 commas;
F, A, C, = 31 commas;
C, E, G, = 31 commas;
G, B, D, = 31 commas;
d, f, a, 8, 5, 9, 8 = 30 commas. - Editor. [Scientific Basis and Build of Music, page 38]
Nature has not finished when she has given us the Diatonic Scale of notes as first generated. In the diatonic scale, in ascending from C, the root of the tonic, the first step is an interval of 9 commas, supposing that we adopt the common division of the octave into 53 commas, which is the nearest practical measuring rule; the second step has 8 commas; the third has 5; the fourth has 9; the fifth has 8; the sixth has 9; and the seventh and last has 5 commas. So we have three steps of 9 commas, two steps of 8, and two of 5. The order of the steps in the major is 9, 8, 5, 9, 8, 9, 5. In the minor the magnitudes are the same, but the order is 9, 5, 8, 9, 5, 9, 8. So there are three magnitudes.1 But Nature has an equalizing process in the course of her musical marshallings, in which these greater ones get cut down, and have to change places with the lesser, when her purpose requires them so to do. [Scientific Basis and Build of Music, page 47]
that Nature has done so.1 And in every new key into which we modulate Nature performs the same operation, till in the course of the twelve scales she has cut every greater note into two, and made the notes of the scale into twelve instead of seven. These we, as a matter of convenience, call semitones; though they are really as much tones as are the small intervals which Nature gave us in the Genesis of the first scale between B-C and E-F. She only repeats the operation for every new key which she had performed at the very first. It is a new key, indeed, but exactly like the first. The 5 and 9 commas interval between E and G becomes a 9 and 5 comma interval; and this Nature does by the rule which rests in the ear, and is uttered in the obedient voice, and not by any mathematical authority from without. She cuts the 9-comma step F to G into two, and leaving 5 commas as the last interval of the new key of G, precisely as she had made 5 commas between B and C as the last interval of the key of C, she adds the other 4 commas to the 5-comma step E to F, which makes this second-last step a 9-comma step, precisely as she had made it in the key of C.2 [Scientific Basis and Build of Music, page 48]
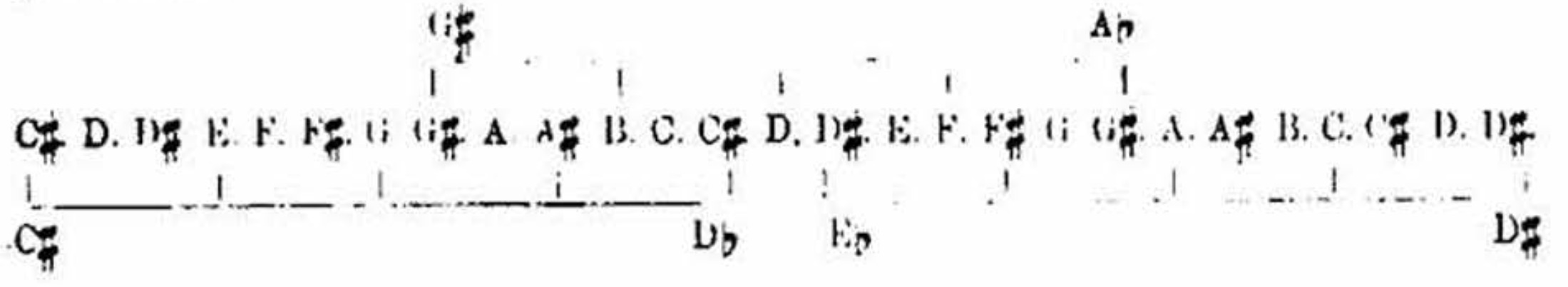
In the above line it will be readily observed that these three chromatic chords, having each of their intervals a minor third, involve, as necessary elements of their build, every one of the twelve semitones at one point or another of the line. This is a second witness to the legitimacy of the chromatic scale of twelve semitones. We have our first witness to the same in the evolution of the semitones progressively in the course of the modulations by which, in growth-like continuity, Nature links the successive keys; whether developed upward, as is the natural way of the majors; or downward, as in the natural way of the minors; or half upward and half downward, which is an expedient in order to simplify the signatures. In whichever direction the modulation is effected, one note is always divided, and must, true to Nature, be signified by placing a sharp or a ?, as the case may be, to the 4-comma altered interval, and this always leaves a 5-comma interval to occupy the place to which Nature has assigned such interval in the original scale. When this operation has been twelve times performed, we have the chromatic scale of twelve semitones. Thus by two witnesses the thing is established. By further examination of these chromatic chords we find other interesting features beside their witness to the twelve semitones of the octave. [Scientific Basis and Build of Music, page 56]
Although the system is composed of only three ratios, which in themselves moreover, are of a very fixed character, yet mobility and variety are chief features among the notes of the system. Great changes are effected by small means. By lowering the second of the major D one comma, the ratio of 80:81, [Scientific Basis and Build of Music, page 61]
The various raisings and lowerings of notes in advancing keys, major and minor. - In each fifth of the majors ascending the top of the dominant is raised a comma. A40 in the key of C becomes A40 1/2 in the key of G; E60 in the scale of G is E60 3/4 in the scale of D; B90 in the scale of D is B91 1/8 in the scale of A. This alteration of the top of the dominant major goes on through all the twelve scales. Similarly, by the Law of Duality, each fifth in the minors descending has the root of the subdominant lowered a comma. D54 in the key of E minor is D53 1/2 in the key of A; G72 in the scale of A is G71 1/9 in the scale of D; C48 in the scale of D is C47 11/27 in the scale of G. This alteration of the root of the subdominant goes on through all the twelve minor scales. [Scientific Basis and Build of Music, page 62]
In just such a manner, only by more obvious leaps, the middle of the dominant in the advancing major scales is raised a sharp - i.e., four commas. When D27, the dominant top of the key of C, is multiplied by 5, it generates F#135; so, taking it one octave lower, F64 in C major is F#67 1/2 in the key of G. C96 in the key of G is C#101 1/4 in the key of D; G72 in the key of D is G#151 7/8 in the key of A. And this raising of the middle of the dominant goes on through all the twelve major keys.[Scientific Basis and Build of Music, page 62]
lastly it is altered again and becomes, by the power of 3 once more, F#,#, and serves in four keys. But this carries us beyond the horizon of our musical world of twelve keys; for in B#, the top of the tonic E, we have reached our twelfth fifth, and it here coalesces with C of the seventh octave, and closes the circle. This is the way that all notes become alternately altered, either by commas and sharps in the upward genesis of scales, or by commas and flats in the downward Genesis, by the alternate powers of 3 and 5. In the upward Genesis in this illustration, notes by the power of 5 serve in three keys, and those by the power of 3 serve in four keys. In the minors it is just the inverse on this by the Law of Duality. But no note serves for more than either three or four keys, as the case may be. [Scientific Basis and Build of Music, page 63]
common, to mingle with more chord-society. So those added thirds which constitute compound chords are like accomplishments acquired for this end, and they make such chords exceedingly interesting. The dominant assumes the root of the subdominant, and so becomes the dominant seventh that it may be affiliated with the subdominant chords. Inversely, the subdominant assumes the top of the dominant chord that it may be affiliated with the dominant. The major tonic may exceptionally be compounded with the top of the minor subdominant when it comes between that chord and its own dominant; and the minor tonic may in the same way assume the root of the major dominant when it comes between that chord and its subdominant. The minor subdominant D F A, and the major dominant G B D, are too great strangers to affiliate without some chord to introduce them; they seem to have one note in common, indeed, but we know that even these two D's are a comma apart, although one piano-key plays them both, and the F G and the A B are as foreign to each other as two seconds can be, each pair being 9 commas apart, and G A are 8 commas apart. In this case, as a matter of musical courtesy, the tonic chord comes in between; and when it is the minor subdominant that is to be introduced, the major tonic assumes the top of that chord, and then turns to its own major dominant and suavely gives the two to enter into fellowship; for the tonic received the minor subdominant through its semitonic E F, and carries it to the major dominant through its semitonic B C, along with C in common on the one side and G in common on the other. When it is the major dominant that is to be introduced to the minor subdominant the minor tonic fulfills the function, only the details are all reversed; it assumes the root of dominant, and by this note in common, and its A in common with its own subdominant, along with the semitonic second B C on the one hand and the semitonic E F on the other, all is made smooth and continuous. The whole of this mediatorial intervention on the part of the tonic is under the wondrous law of assimilation, which is the law of laws all through creation; but when the tonic chord has fulfilled this graceful action, it immediately drops the assumed note, and closes the cadence in its own simple form.1 [Scientific Basis and Build of Music, page 71]
If it be asked why no more primes than 2, 3, and 5 are admitted into musical ratios, one reason is that consonances whose vibrations are in ratios whose terms involve 7, 11, 13, etc., would be less simple and harmonious than those whose terms involve the lesser primes only. Another reason is this - as perfect fifths and other intervals resulting from the number 3 make the schism of a comma with perfect thirds and other intervals resulting from the number 5, so intervals resulting from the numbers 7, 11, 13, etc., would make other schisms with both those kinds of intervals. [Scientific Basis and Build of Music, page 75]
There is no one musical interval which is the perfect measuring rule for the others. But the octave has been divided into 53 parts called commas, and these commas are as near a commensurable rule as we need seek for measuring the musical intervals; always remembering that, strictly speaking, these intervals are incommensurable. The large second has 9 commas; the medium second has 8; and the small second 5; and all other intervals, being of course composed of some of these seconds, can be measured accordingly. Thus the comma, though not itself an interval of our musical system, is the handy and sufficiently perfect inch, let us call it, for practical purposes in music. [Scientific Basis and Build of Music, page 75]
The root of the subdominant is F, in the key of C major; and the top of the dominant is D. The difference between these two notes at the top and bottom of the chord-scale, is the quantity which two octaves is more than three fifths; it is the ratio of 27 to 30, a comma less than the minor third whose ratio is 5 to 6. [Scientific Basis and Build of Music, page 76]
At the first, in the laws of quantities and motions adjusting musical vibrations, there is one chord of the three notes, F, A, C, the root, middle, and top of the five notes which compose the true natural scale; this one chord can be reproduced a fifth higher, C, E, G, in the same mathematical form, taking the top of the first for the root of the second chord. In like manner this second can be reproduced another fifth higher, G, B, D, still in the same mathematical form, and so fit to be a member of the chord-scale of a key. But the law does not admit of another reproduction without interfering with the first chord, so that a fourth fifth produces no new effect; but the whole key is simply a fifth higher, i.e., if the fourth fifth has been properly produced by multiplying the top of the third fifth by 3 and by 5, the generating primes in music. That this carries us into a new scale is seen in that the F is no longer the F? but F#, and the A is no longer A? but A,. But if we suppose the fourth fifth to be simply the old notes with their own vibration numbers, then D, F, A would not be a fifth belonging either to the major or the minor mode, but a fifth a comma less. The letters of it would read like the minor subdominant, D, F, A; but the intervals, as found in the upward development of the major genesis, instead of being, when expressed in commas, 9, 5, 8, 9, which is the minor subdominant, would be 8, 5, 9, 8, which is not a fifth of the musical system; these having always, whether major or minor, two 9's, one [Scientific Basis and Build of Music, page 77]
8, and one 5, making 31 commas, while this supposed fourth-fifth major would only have 30. The fifths of the musical system are thus strictly kept as a symbol of the Trinity of the Creator, Three in One. [Scientific Basis and Build of Music, page 78]
The simple natural scale is the fifth; the compound natural scale is the octave; the harmony scale, or chord-scale, is the three fifths; the great genetic scale is six octaves; for, like the six creation days, it takes the six octaves to give birth to the elements of which the wondrous structure of our music is built up; the birthplace of B, the seventh of the octave scale, is the sixth octave of the great genetic scale. The area of the twelve major and twelve minor scales is twelve fifths or seven octaves, the twelfth fifth being a comma and the apotome minor in advance of the seventh octave. This is a quantity so small that it can be ignored in real music; and the two notes, say E# and F, joined to close the circle of this horizon of our music world. E# is the top of the twelfth fifth, and F is the top of the seventh octave; and they are practically, though not exactly mathematically, the same note. Illustrations of this will be found among the plates of this work. [Scientific Basis and Build of Music, page 79]
G# as it occurs in the scales of A, E, and B major, and A? as it occurs in the scales of F and B? minor, are only distant the apotome minor, and are well represented by one key of the piano. It is only G# as it occurs in the scale of F six sharps major, and A? as it occurs in the scale of E six flats minor, that is not represented on the piano. These two extreme notes F# and E? minor are at the distance of fifteenth fifths and a minor third from each other. This supplies notes for 13 major and 13 minor mathematical scales; but as this is not required for our musical world of twelve scales, so these far-distant G# and A? are not required. The piano is only responsible for the amount of tempering which twelve fifths require, and that is never more than one comma and the apotome minor. [Scientific Basis and Build of Music, page 80]
Having found the framework of the major scale by multiplying F1 three times by 3, find the framework of the minor by dividing three times by 3. But what shall we divide? Well, F1 is the unbegotten of the 25 notes of the great genetic scale; B45 is the last-born of the same scale. We multiply upward from F1 for the major; divide downward from B45 for the minor. Again, B45 is the middle of the top chord of the major system, a minor third below D, the top of that chord, and the top of the whole major chord-scale, so B is the relative minor to it. Now since the minor is to be seen as the INVERSE of the major, the whole process must be inverse. Divide instead of multiply! Divide from the top chord instead of multiply from the bottom chord. Divide from the top of the minor dominant instead of multiply from the root of the major subdominant. This will give the framework of the minor system, B45/3 = E15/3 = A5/3 = D1 2/3. But as 1 2/3 is not easily compared with D27 of the major, take a higher octave of B and divide from it. Two times B45 is B90, and two times B90 is B180, and two times B180 is B360, the number of the degrees of a circle, and two times B360 is B720; all these are simply octaves of B, and do not in the least alter the character of that note; now B720/3 is = E240/3 = A80/3 = D26 2/3. And now comparing D27 found from F1, and D26 2/3 found from B720, we see that while E240 is the same both ways, and also A80, yet D26 2/3 is a comma lower than D27. This is the note which is the center of the dual system, and it is itself a dual note befittingly. [Scientific Basis and Build of Music, page 81]
So the dual system of Music revolves round a mathematical point which is in none of its notes, but in the empty space between the two D's. Like the earth, it is hung upon nothing. This is an exceedingly interesting musical phenomenon. In that comma of vacant space is music's center of gravity.
1 3 9 27
F C G D
D A E B
26 2/3 80 240 720 [Scientific Basis and Build of Music, page 82]
N.B. - The sharp comes here by the prime 5, and the comma by the prime 3. Now we have the key of G provided for;-

These are two octaves of the scale of G. G A B, which in the scale of C was an 8-9-comma third, must now take the place of C D E, which in C was a 9-6-comma [Scientific Basis and Build of Music, page 82]
third; and in order to do so, A has been mathematically raised a comma, which makes G A B now a 9-8 comma third. E F G, which in the scale of C was a 5-9 comma third, must now take the place of A B C in the scale of C, which was a 9-5 comma third; and in order to do so, F is mathematically raised 4 commas, and must be marked F#; and now the interval is right for the scale of G. E F# G is a 9-5 comma interval. This mathematical process, in the majors, puts every scale in its original form as to vibration-numbers; but since the same letters are kept for the naming of the notes, they must be marked with commas or sharps, as the case may be. In the Sol Fa notation such marks would not be necessary, as Do is always the key-note, Ray always the second, and Te always the seventh. [Scientific Basis and Build of Music, page 83]
N.B. - The flat comes here by the prime 5, and the comma by the prime 3. Now we have the key of D provided for:-
The interval F G A, which in the scale of A was a 9-8-comma interval, must take the place of C D E of the scale of A, which is an 8-9-comma interval; and in order to do this, G has been mathematically lowered a comma. As the middle of the dominant in the major is raised a comma, so the root of the subdominant is lowered a comma. The interval A B C, which in the scale of A was a 9-5-comma interval, is here to take the place of E F G in the scale of A, which is a 5-9-comma interval; and in order to do so, B is lowered 4 commas, and so becomes ?B; and this mathematical process makes the new scale exactly like the old one. This is the way of the minors when calculated as a descending series of scales, which is their natural way. [Scientific Basis and Build of Music, page 84]
There are 32 notes required for each octave for the 13 major and the 13 minor mathematical scales. These 32 notes are by the law of duality arranged symmetrically from D as a center upwards to G#, and downwards to A?. D itself serves for 2 of the 32 on the piano. The first black keys on each side of D serve for nominally 3 notes each = 6. The first white key above and the first below D serve for 2 notes each = 4. The second white key above and the second below serve each for 3 notes = 6. The second black keys above and below D serve each for 3 notes = 6. The third black key above D is G#, the third below is A?; this key, for it is one, serves for 2 of the 32. There is a comma of difference between D minor and D major. Six fifths below the minor D26 2/3 is A?, the root of the subdominant of the key of E? minor; and six fifths above the major D27 is G#, the top of the dominant of F# major. The difference between this minor A? and this major G# is two commas and [Scientific Basis and Build of Music, page 85]
the apotome minor; but one of these is the original comma which is genetically between the two D's; and it occurs here again at the 13th scale, the first of a new circle; it really corresponds to the two D's at the beginning of this first series. Whenever there is more than one comma and the apotome minor between G# and A?, it is because there has been a mistake in counting this one over again; or some other mistake. [Scientific Basis and Build of Music, page 86]
And it is another very interesting fact that those numbers multiplied into each other always make 720, the number in the minor genesis which corresponds to 1 in the major; F1 being the generative root of the major, and B720 the generative top of the minor; so adjusted they place the two D's beside each other - D26 2/3 and D27 - and we see the comma of difference between these two numbers which are distinctive of the major and the minor; 26 2/3 x 3 = 80, and 27 x 3 = 81, and 80:81 is the ratio of the comma. This is the Ray and the Rah in which there lurks one of music's mysteries. Let him that is wise unravel it. It is symbolic of something in the spiritual realm of things; its full meaning is only found there. [Scientific Basis and Build of Music, page 88]
Seven notes in the Octave are required for the major scale, e.g., the scale of C. All the notes of the relative minor A are the same as those of the scale of C major, with exception of D, its fourth in its Octave scale, and the root of its subdominant in its chord-scale; thus, one note, a comma lower for the D, gives the scale of A minor. [Scientific Basis and Build of Music, page 88]
The reason why there are 13 mathematical scales is that G? and F# are written separately as two scales, although the one is only a comma and the apotome minor higher than the other, while in the regular succession of scales the one is always 5 notes higher than the other; so this G? is an anomaly among scales, unless viewed as the first of a second cycle of keys, which it really is; and all the notes of all the scales of this second cycle are equally a comma and the apotome higher than the notes of the first cycle; and when followed out we find that a third cycle is raised just as much higher than the second as the second is higher than the first; and what is true of these majors may be simply repeated as to the D# and E? of the minors, and the new cycle so begun, and all successive minor cycles. Twelve and not thirteen is the natural number for the mathematical scales, which go on in a spiral line, as truly as for the tempered scales, which close as a circle at this point. [Scientific Basis and Build of Music, page 89]
In a musical air or harmony, i.e., when once a key has been instituted in the ear, all the various notes and chords seem animated and imbued with tendency and motion; and the center of attraction and repose is the tonic, i.e., the key-note or key-chord. The moving notes have certain leanings or attractions to other notes. These leanings are from two causes, local proximity and native affinity. The attraction of native affinity arises from the birth and kindred of the notes as seen in the six-octave genesis, and pertains to their harmonic combinations. The attraction of local proximity arises from the way the notes are marshalled compactly in the octave scale which appears at the head of the Genesis, and pertains to their melodic succession. In this last scale the proximities are diverse; the 53 commas of the octave being so divided as to give larger and lesser distances between the notes; and of course the attraction of proximity is strongest between the nearest; a note will prefer to move 5 commas rather than 8 or 9 commas to find rest. Thus far PROXIMITY. [Scientific Basis and Build of Music, page 91]
In the opening of the third measure the tune returns to its own key by striking the tonic. This case is a very simple illustration of how a composition will move with perfect naturalness in more keys than one, the keys so grow out of each other, and may either merely snatch a passing chord from a new key, or pass quite into it for a phrase or two, or for a whole measure, then return as naturally, either by a smooth and quiet or by a strongly contrasted turn, according to the chords between which the turn takes place. In such modulation there may or there may not be marked a sharp, ?, or ?, in the air itself; the note which Nature raises in the new key may occur in one of the other parts of the harmony. In Watchman it is A, the fourth, which is altered; from being ? it is made ?. The change which takes place in the sixth of the scale, which is C in Watchman, is only one comma, the ratio of 80 to 81, and it slips into the new key as if nothing had happened. No mark is placed to it, as the comma difference is never taken notice of, although it is really and regularly taking place, with all the precision of Nature, in every new key. It is, however, only the note which is altered four commas, which is marked by a sharp, ?, or ?, as the case may be. [Scientific Basis and Build of Music, page 94]
VIOLIN-FINGERING - Whenever the third finger is normally fourth for its own open string, then the passage from the third finger to the next higher open string is always in the ratio of 8:9; and if the key requires that such passage should be a 9:10 interval, it requires to be done by the little finger on the same string, because the next higher open string is a comma too high, as would be the case with the E string in the key of G.
In the key of C on the violin you cannot play on the open A and E strings; you must pitch all the notes in the scale higher if you want to get [Scientific Basis and Build of Music, page 99]
the use of these two open strings in the key of C, on account of the intervals from G to A and from D to E being the ratio of 9:10, the medium second in the scale. G, the third finger on the third string, to A, the open second string, and D, the third finger on the second string, to E, the open first string, being in ratio of 8:9, the large second, you must either use the fourth finger for A and E, or use all the other notes a comma higher. But if thus you use all the notes a little higher, so as to get the use of the A and E strings open, then you cannot get the use of the G and D strings open. On the other hand, in this key of C, if you use the G and D strings open, you cannot use the A and E strings open. One might think the cases parallel, but they are not; because you have a remedy for the first and second open strings, but no remedy for the other two. The remedy for the first and second open strings is to put the fourth finger on the second and third strings for the E and A; but it would be inconvenient, if not impossible, to use the other two strings, G and A, by putting the first finger a comma higher than the open string. [Scientific Basis and Build of Music, page 100]
Whenever a sharp comes in in making a new key - that is, the last sharp necessary to make the new key - the middle of the chord in major keys with sharps is raised by the sharp, and the top of the same chord by a comma. Thus when pausing from the key of C to the key of G, when F is made sharp A is raised a comma. When C is made sharp in the key of D, then E is raised a comma, and you can use the first open string. When G is made sharp for the key of A, then B is raised a comma. When D is made sharp for the key of E, then F# is raised a comma; so that in the key of G you can use all the open strings except the first - that is, E. In the key of D you can use all the open strings. In the key of A you can use the first, second, and third strings open, but not the fourth, as G is sharp. In the key of E you can use the first and second open. [Scientific Basis and Build of Music, page 100]
In the lowest Fig. this framework is filled up with all the octaves of the notes found as in the top Fig., the major being evolved upward and the minor downward, and the two systems centered at the D's, which are shown a comma distant from each other. [Scientific Basis and Build of Music, page 103]
Fig. 1 - The pendulums in this illustration are suspended from points determined by the division of the Octave into Commas; the comma-measured chords of the Major key being S, 9, 8, 9, 5; T, 9, 8, 5, 9; D, 8, 9, 5, 9. The pendulums suspended from these points are tuned, as to length, to swing the mathematical ratios of the Diatonic scale. The longest pendulum is F, the chords being properly arranged with the subdominant, tonic, and dominant, the lowest, center, and upper chords respectively. Although in "Nature's Grand Fugue" there are 25 pendulums engaged, as will be seen by reference to it, yet for the area of a single key 13 pendulums, as here set forth, are all that are required. It will not fail to be observed that thus arranged, according to the law of the genesis of the scale, they form a beautiful curve, probably the curve of a falling projectile. It is an exceedingly interesting sight to watch the unfailing coincidences of the pendulums perfectly tuned, when started in pairs such as F4, A5, and C6; or started all together and seen in their manifold manner of working. The eye is then treated to a sight, in this solemn silent harp, of the order in which the vibrations of sounding instruments play their sweet coincidences on the drum of the delighted ear; and these two "art senses," the eye and the ear, keep good company. Fig. 2 is an illustration of the correct definition of a Pendulum Oscillation, as defined in this work. In watching the swinging pendulums, it will be observed that the coincidences [Scientific Basis and Build of Music, page 104]
This plate is a representation of the area of a scale; the major scale, when viewed with the large hemisphere, lowest; the minor when viewed the reverse way. It is here pictorially shown that major and minor does not mean larger and smaller, for both modes occupy the same area, and have in their structure the same intervals, though standing in a different order. It is this difference in structural arrangement of the intervals which characterizes the one as masculine and the other as feminine, which are much preferable to the major and minor as distinctive names for the two modes. Each scale, in both its modes, has three Fifths - subdominant, tonic, and dominant. The middle fifth is the tonic, and its lowest note the key-note of the scale, or of any composition written in this scale. The 53 commas of the Octave are variously allotted in its seven notes - 3 of them have 9 commas, 2 have 8, and 2 have 5. The area of the scale, however, has much more than the octave; it is two octaves, all save the minor third D-F, and has 93 commas. This is the area alike of masculine and feminine modes. The two modes are here shown as directly related, as we might figuratively say, in their marriage relation. The law of Duality, which always emerges when the two modes are seen in their relationship, is here illustrated, and the dual notes are indicated by oblique lines across the pairs. [Scientific Basis and Build of Music, page 106]
The larger hemisphere of the Fifths is uppermost when taking the minor view of the plate, and suggests the idea of the minor being weighed downward, as it really is mathematically in the genesis of the scale, which is seen in the D of the minor being a comma lower than the D of the major. Taking the major view of the plate, the smaller hemisphere is uppermost, and suggest the idea of rising upward, as it really does in the [Scientific Basis and Build of Music, page 106]
mathematical genesis, as seen in its D being a comma higher than that of the minor. This gravity and buoyancy of the modes is a striking feature of them. In the Thirds it is different from the Fifths; the larger hemisphere of each third seems gravitating toward the center of the tonic chord. The area of the scale has then the aspect of a planet with its north and south poles, and pervaded by a tendency towards the center; the center itself being neutral as to motion. [Scientific Basis and Build of Music, page 107]
When Leonhard Euler, the distinguished mathematician of the eighteenth century, wrote his essay on a New Theory of Music, Fuss remarks - "It has no great success, as it contained too much geometry for musicians, and too much music for geometers." There was a reason which Fuss was not seemingly able to observe, namely, that while it had hold of some very precious musical truth it also put forth some error, and error is always a hindrance to true progress. Euler did good service, however. In his letters to a German Princess on his theory of music he showed the true use of the mathematical primes 2, 3, and 5, but debarred the use of 7, saying, "Were we to introduce the number 7, the tones of an octave would be increased." It was wise in the great mathematician to hold his hand from adding other notes. It is always dangerous to offer strange fire on the altar. He very clearly set forth that while 2 has an unlimited use in producing Octaves, 3 must be limited to its use 3 times in producing Fifths. This was right, for in producing a fourth Fifth it is not a Fifth for the scale. But Euler erred in attempting to generate the semitonic scale of 12 notes by the use of the power of 5 a second time on the original materials. It produces F# right enough; for D27 by 5 gives 135, which is the number for F#. D27 is the note by which F# is produced, because D is right for this process in its unaltered condition. But when Euler proceeds further to use the prime 5 on the middles, A, E, and B, and F#, in their original and unaltered state, he quite errs, and produces all the sharpened notes too low. C# for the key of D is not got by applying 5 to A40, as it is in its birthplace; A40 has already been altered for the key of G by a comma, and is A40 1/2 before it is used for producing its third; it is A40 1/2 that, multiplied by 5, gives C#202 1/2, not C200, as Euler makes C#. Things are in the same condition with E before G# is wanted for the key of A. G# is found by 5 applied to E; not E in its original and unaltered state, E30; but as already raised a comma for the key of D, E30 3/8; so G# is not 300, as Euler has it, but 303 3/4. Euler next, by the same erroneous methods, proceeds to generate D# from B45, its birthplace number; but before D# is wanted for the key of E, B has been raised a comma, and is no longer B45, but B45 9/16, and this multiplied by 5 gives D#227 13/16, not D225, as Euler gives it. The last semitone which he generates to complete his 12 semitones is B?; that is A#, properly speaking, for this series, and he generates it from F#135; but this already altered note, before A# is wanted for the key of B, has been again raised a comma [Scientific Basis and Build of Music, page 107]
for the key of E, and is no longer F#135, but F#136 11/16; and so A# produced by 5 from F#136 11/16, as Euler has it, but A#683 7/16, A itself having been already raised a comma before it comes to be sharpened. So Euler's chromatic scale of 12 semitones is all wrong except F#, which, by accident, is right.1 [Scientific Basis and Build of Music, page 108]
In the center column are the notes, named; with the lesser and larger steps of their mathematical evolution marked with commas, sharps, and flats; the comma and flat of the descending evolution placed to the left; the comma and sharp of the ascending evolution to the right; and in both cases as they arise. If a note is first altered by a comma, this mark is placed next to the letter; if first altered by a sharp or flat, these marks are placed next the letter. It will be observed that the sharpened note is always higher a little than the note above it when flattened; A# is higher than ?B; and B is higher than ?C, etc.; thus it is all through the scales; and probably it is also so with a fine voice guided by a true ear; for the natural tendency of sharpened notes is upward, and that of flattened notes downward; the degree of such difference is so small, however, that there has been difference of opinion as to whether the sharp and ? have a space between them, or whether they overlap, as we have shown they do. In tempered instruments with fixed keys the small disparity is ignored, and one key serves for both. In the double columns right and left of the notes are their mathematical numbers as they arise in the Genesis of the scales. In the seven columns right of the one number-column, and in the six on the left of the other, are the 12 major and their 12 relative minor scales, so arranged that the mathematical number of their notes is always standing in file with their notes. D in A minor is seen as 53 1/3, while the D of C major is 54; this is the comma of difference in the primitive Genesis, and establishes the sexual distinction of major and minor all through. The fourth of the minor is always a comma lower than the second of the major, though having the same name; this note in the development of the scales by flats drops in the minor a comma below the major, and in the development of the scales by sharps ascends in the major a comma above the minor. In the head of the plate the key-notes of the 12 majors, and under them those of their relative minors, are placed over the respective scales extended below. This plate will afford a good deal of teaching to a careful student; and none will readily fail to see beautiful indications of the deep-seated Duality of Major and Minor. [Scientific Basis and Build of Music, page 109]
ratio of 5:8; three, 3:5; and one, 16:27. There are seven fifths - one in the ratio of 45:64; one, 27:40; and five, 2:3; and seven corresponding fourths - five in the ratio 3:4; one, 40:54; and one 32:45. These are the ratios of the intervals in their simplest expressions as given in the second outer space above the staff in the plate. In the outer space the intervals are given less exactly, but more appreciable, in commas. The ratios of the vibration-numbers of each interval in particular, counting from C24, are given in the inner space above the staff. These vibration-numbers, however, are not given in concert pitch of the notes, but as they arise in the low audible region into which we first come in the Genesis from F1, in the usual way of this work. The ratios would be the same at concert pitch; Nature gives the numbers true at whatever pitch in the audible range, or in the low and high silences which lies out of earshot in our present mortal condition. [Scientific Basis and Build of Music, page 110]
When the major and minor scales are generated to be shown the one half in #s and the other half in ?s, it is not necessary to carry the mathematical process through the whole 24, as when the majors are all in #s and the minors all in ?s; because when six majors have been generated in #s, they furnish the new notes needed by the six relative minors; and when six minors have been generated in ?s, they furnish the new notes for the six relative majors. This plate begins with the major in C and the minor in A. The notes of these two are all identical except the D, which is the sexual note, in which each is not the other, the D of the minor being a comma lower than the D of the major. Going round by the keys in #s, we come first to E minor and G major. G major has been mathematically generated, and the relative minor E gets its F# from it; but the D of C major must also be [Scientific Basis and Build of Music, page 112]
given to this scale, as the D of A minor would be a comma too low; it would make a 9-comma interval between D and E, the seventh and eighth, where the minor mode has an 8-comma one. So its two new notes are thus found in the relative and sub-relative majors. This is the way of their mutual providing in the region of the #s; the # seventh of the major is given to be the # second of the minor, and the comma-higher second of the sub-relative becomes the seventh of the minor; and then we have a true written representation of what Nature has done. [Scientific Basis and Build of Music, page 113]
Starting again at C major and A minor and going round by the keys in ?s, we come first to D minor and F major. The major gets its ? fourth from the ? sixth of the relative minor; and as the interval between D-E, the major sixth and seventh, must be a 9-comma interval, and its own D-E is only an 8-comma one, it must take the D of A minor, which is a comma lower, and this will correctly show the 9-comma interval between D and E. This is the way of their mutual providing in the region of ?s; the ? sixth of the minor is given to be the ? fourth of the relative major; and the comma-lower fourth of the sub-relative minor becomes the correct sixth of the major. The arrows indicate the source from which, and the place to which; the new notes come and go. [Scientific Basis and Build of Music, page 113]
The Octave being divided into 53 commas, the intervals are measured, as usual, by these, the large second having 9-commas, the medium second having 8, and the small second 5. These measures are then made each the radius by which to draw hemispheres showing the various and comparative areas of the seconds. The comparative areas of the thirds are shown by the hemispheres of the seconds which compose them facing each other in pairs. The comma-measures of the various thirds thus determined are then made the radii by which to draw the two hemispheres of the fifths. The areas of the three fifths are identical, as also the attitudes of their unequal hemispheres. The attitude of the six thirds, on the other hand, in their two kinds, being reversed in the upper and under halves of the scale, their attitude gives them the appearance of being attracted towards the center of the tonic; while the attitude of the three fifths is all upward in the major, and all downward in the minor; their attraction being towards the common center of the twelve scales which Nature has placed between the second of the major and the fourth of the minor, as seen in the two D's of the dual genetic scale, - the two modes being thus seen, as it were, revolving [Scientific Basis and Build of Music, page 113]
When Plate XIII. is divided up the middle of the column, as in Plate XIV., so as that one side may be slipped up a fifth, representing a new key one-fifth higher, its subdominant made to face the old tonic, the two new notes are then pictorially shown, the second being altered one comma and the seventh four commas. The key at this new and higher pitch is by Nature's unfailing care kept precisely in the same form as the first; and wherever the major scale is pitched, higher or lower, the form remains unaltered, all the intervals arranging themselves in the same order. The ear, and the voice obedient to it, carry Nature's measuring-rule in them, and the writing must use such marks as may truly represent this; hence the use of sharps, flats, and naturals; these, however, be it observed, are only marks in the writing; all is natural at any pitch in the scale itself. All this is equally true of the minor mode at various pitches. These two plates are only another and more pictorial way of showing what the stave and the signature are usually made to express. [Scientific Basis and Build of Music, page 114]
The middle portion with the zigzag and perpendicular lines are the chromatic chords, as it were arpeggio'd. They are shown 5-fold, and have their major form from the right side, and their minor form from the left. In the column on the right they are seen in resolution, in their primary and fullest manner, with the 12 minors. The reason why there are 13 scales, though called the 12, is that F# is one scale and G? another on the major side; and D# and E? separated the same way on the minor side. Twelve, however, is the natural number for the mathematical scales as well as the tempered ones. But as the mathematical scales roll on in cycles, F# is mathematically the first of a new cycle, and all the notes of the scale of F# are a comma and the apotome minor higher than G?. And so also it is on the minor side, D# is a comma and the apotome higher than E?. These two thirteenth keys are therefore simply a repetition of the two first; a fourteenth would be a repetition of the second; and so on all through till a second cycle of twelve would be completed; and the thirteenth to it would be just the first of a third cycle a comma and the apotome minor higher than the second, and so on ad infinitum. In the tempered scales F# and G? on the major side are made one; and D# and E? on the minor side the same; and the circle of the twelve is closed. This is the explanation of the thirteen in any of the plates being called twelve. The perpendicular lines join identical notes with diverse names. The zigzag lines thread the rising Fifths which constitute the chromatic chords under diverse names, and these chords are then seen in stave-notation, or the major and minor sides opposites. The system of the Secondary and Tertiary manner of resolution might be shown in the same way, thus exhibiting 72 resolutions into Tonic chords. But the Chromatic chord can also be used to resolve to the Subdominant and Dominant chords of each of these 24 keys, which will exhibit 48 more chromatic resolutions; and resolving into the 48 chords in the primary, secondary, and tertiary manners, will make 144 resolutions, which with 72 above make 216 resolutions. These have been worked out by our author in the Common Notation, in a variety of positions and inversions, and may be published, perhaps, in a second edition of this work, or in a practical work by themselves. [Scientific Basis and Build of Music, page 115]
This is a twofold mathematical table of the masculine and feminine modes of the twelve scales, the so-called major and relative minor. The minor is set a minor third below the major in every pair, so that the figures in which they are the same may be beside each other; and in this arrangement, in the fourth column in which the figures of the major second stand over the minor fourth, is shown in each pair the sexual note, the minor being always a comma lower than the major. An index finger points to this distinctive note. The note, however, which is here seen as the distinction of the feminine mode, is found in the sixth of the preceding masculine scale in every case, except in the first, where the note is D26 2/3. D is the Fourth of the octave scale of A minor, and the Second of the octave scale of C major. It is only on this note that the two modes differ; the major Second and the minor Fourth are the sexual notes in which each is itself, and not the other. Down this column of seconds and fourths will be seen this sexual distinction through all the twelve scales, they being in this table wholly developed upward by sharps. The minor is always left this comma behind by the comma-advance of the major. The major A in the key of C is 40, but in the key of G it has been advanced to 40 1/2; while in the key of E, this relative minor to G, the A is still 40, a comma lower, and thus it is all the way through the relative scales. This note is found by her own downward Genesis from B, the top of the feminine dominant. But it will be remembered that this same B is the middle of the dominant of the masculine, and so the whole feminine mode is seen to be not a terminal, but a lateral outgrowth from the masculine. Compare Plate II., where the whole twofold yet continuous Genesis is seen. The mathematical numbers in which the vibration-ratios are expressed are not those of concert pitch, but those in which they appear in the genesis of the scale which begins from F1, for the sake of having the simplest expression of numbers; and it is this series of numbers which is used, for the most part, in this work. It must not be supposed, however, by the young student that there is any necessity for this arrangement. The unit from which to begin may be any number; it may, if he chooses, be the concert-pitch-number of F. But let him take good heed that when he has decided what his unit will be there is no more coming and going, no more choosing by him; Nature comes in [Scientific Basis and Build of Music, page 117]
This diagram shows pictorially the open in the spiral of the mathematical scales, in which, if written in sharps only, B# is seen a little, that is, a comma and the apotome minor, in advance of C, and as the first scale of the new cycle; for it is a violation of Nature's beautiful steps to call it a thirteenth scale of this order, since every scale in the order is 31 commas in advance of the preceding, whereas B# is only one comma and a small fraction in advance of C. If the scales be written in ?s and #s for convenience of signature, then G# is seen a comma and apotome in advance of A?; while the whole circle of keys advancing by fifths are each 31 commas in advance of the preceding. We may therefore cast utterly from us the idea of there being more than twelve mathematical scales, and view the so-called thirteenth as simply the first of a new round of the endless spiral of scales. There is, however, in this note a banner with the strange device, "Excelsior," for it leads us onward into ever-advancing regions of vibrations, and would at last bring us to the ultimate and invisible dynamic structure of the visible world. The tempered system of 12 keys, as in Fig. 1, is by causing the G# and A? to coalesce and be one, as the two D's are already literally one by Nature's own doing. [Scientific Basis and Build of Music, page 118]
This plate sets forth the essential duality of the musical system of vibrations. It is a remarkable fact that the numbers of the vibrations of the major mode are the numbers for the string proportions of the minor mode; and vice versa, the string proportions in the major are the numbers of the vibrations in the minor. We have, however, to see that we use the proper notes and numbers; we must know the secret of Nature. This secret rests in the duality of the notes, and begins from the two D's. The center of gravity of the musical system of vibrations is found in the comma space between the two D's as they are found in the Genesis of the two modes. In these two D's the vibration number and string proportions are nearly identical. Starting from this point as the center of gravity in the [Scientific Basis and Build of Music, page 118]
This plate, in the outer stave, has the 32 notes which arise with mathematical development of twelve scales in advancing fifths. The notes are marked with sharps, flats, and commas. The flats and commas of lowering are placed on the left of the notes, in the order in which they arise, reading them from the note downward; the sharps and commas of rising on the right, also reading from the note upward. The whole of these 32 notes are brought within the compass of an octave. [Scientific Basis and Build of Music, page 119]
Fig. 1. - This figure shows the major and minor measured in commas and placed directly as they stand related, major and relative minor, the minor being set a minor third lower than the major. The interval between C and E in the minor is an 8-and-9-comma interval; between C and E in the major it is a 9-and-8-comma one. This difference arises from the minor D being a comma lower than the major D. In all the other intervals minor and major are the same. [Scientific Basis and Build of Music, page 120]
See Also
5-comma
8-comma
9-comma
12.18 - Multiple Octave Progression
Alphanon
Apotome Minor
Apotome
arithmetic progression
arithmetical progression
Atom
Atomoles
change
comma-advance
constant of energy
constants of energy
delta
Diesis
enharmonic diesis
evolution
Figure 15.00c - Keelys Devices for Liberating and Measuring Etheric Pressure
flat
Geometrical Progression
harmonic progression
interval
Interval
inverse progression
light units
Measure
measurement
MEASURING THE VELOCITY OF THE ETHERIC CAPSULE
musical progression
progression of adjacencies
progression of keys
progression
Pythagorean Comma
Pythagorean Komma
Ramsay - PLATE XXVII - The Mathematical Scale of Thirty two notes in Commas, Sharps and Flats
reciprocal progression
semitone
semitonic progression
sharp
Sound Measurements
Step
step
Test and Measurement
Thought
TREXNONAR MEASUREMENT OF MOLECULAR OSCILLATING FREQUENCIES
unit of Creation
unit of motions
unit of quantities
Unit
units of electric motion
unity of effect
unity of structure
Universal Energy Unit
wave unit
Wave
