A musical ratio of 6:5, generally speaking.
Keely
All abnormal discordant aggregations in these resonating convolutions produce differentiation to concordant transmission; and according as these differentiations exist in volume, so the transmissions are discordantly transferred, producing antagonism to pure physical action. Thus, in motor ataxy, a differentiation of the minor thirds of the posterior parietal lobule produces the same condition between the retractors and extendors of the leg and foot, and thus the control of the proper movements is lost through this differentiation. The same truth can be universally applied to any of the cerebral convolutions that are in a state of differential harmony to the mass of immediate cerebral surroundings. Taking the cerebral condition of the whole mass as one, it is subservient to one general head centre; although as many neutrals are represented as there are convolutions. The introductory minors are controlled by the molecular; the next progressive third by the atomic; and the high third by the etheric. All these progressive links have their positive, negative, and neutral position. When we take into consideration the structural condition of the human brain, we ought not to be bewildered by the infinite variety of its sympathetic impulses, inasmuch as it unerringly proves the true philosophy that the mass-chords of such structures are governed by vibratory etheric flows. There is no structure whatever - animal, vegetable, or mineral - that is not built up from the cosmic ether. Certain orders of attractive vibration produce certain orders of structure; thus the infinite variety of effects; more especially in the cerebral organs. Discordance cannot exist in the molecule proper. Discordance in any mass is the result of differentiated groups induced by antagonistic chords, and any differentiated mass can be brought to a condition of harmony or equation by proper chord media, and an equated sympathy produced whether the mass be metal or brain. [Vibratory Physics - The Connecting Link between Mind and Matter]
Ramsay
In order to find the notes for the next major key above C, we have to multiply the vibration-number of D, which is the top of the dominant C, by 3 and 5. It is out of the key of C at this point that the new key sprouts and grows, and by the primes and method which produce the key of C itself. So if we would find the relative minor of C, let us take the note which is a minor third below D - that is, B - to produce the minor. The minor sprouts and grows from this point of the key of C; for the relative minor grows out of the major, as out of the man at first the woman is taken. Moreover, B is the last-born of the notes for the major scale; for the middles, that is, the thirds of chords, are always produced by the prime 5; and the tops, that is, the fifths of chords, are produced by the prime 3, and are born before the thirds, though placed after them in the chords. Well, because B is the last-born note of the major, as well as a minor third below the top of the highest chord of the major, it seems that the minor should have this for its point of departure. Again, we have seen that the major and the minor are found in their strings and their vibrations by an inverse process, that one going back upon the other; and, there taking Nature's clue, let us proceed by an inverse process of generating the minor. Making B45 our unit, as F1 was our unit for the major, let us divide by 3 and 5 for a root and middle to B, as we multiplied by 3 and 5 for a top and middle to F. B45 divided by 3 is 15; here then is our E, the root of the chord, just where we had found it coming upward; for, remember, we found E15 by multiplying C3 by 5. This E, then, is the same in major and minor. Now B45 divided by 5 is 9; [Scientific Basis and Build of Music, page 31]
The major scale is composed of three fifths with their middle notes, that is to say, their thirds. And as three such fifths are two octaves, less the small minor third D to F, taking the scale of C for example, so these three fifths are not joined in a circle, but the top of the dominant and the root of the subdominant are standing apart this much, that is, this minor third, D, e, F. Had they been joined, the key would have been a motionless system, with no compound chords, and no opening for modulation into other keys. [Scientific Basis and Build of Music, page 38]
The triplet B, D, F, has been called the imperfect triad, because in it the two diatonic semitones, B-C and E-F, and the two minor thirds which they constitute, come together in this so-called imperfect fifth. But instead of deserving any name indicating imperfection, this most interesting triad is the Diatonic germ of the chromatic chord, and of the chromatic system of chords. Place this triad to precede the tonic chord of the key of C major, and there are two semitonic progressions. Place it to precede the tonic chord of the key of F# major, and there are three semitonic progressions. Again, if we place it to precede the tonic chord of the key of A minor, there are two semitonic progressions; but make it precede the tonic chord of E? minor, and there are three semitonic progressions. This shows that the chromatic chord has its germ in, and its outgrowth from the so-called "natural notes," that is notes without flats or sharps, notes with white keys; and that these natural notes furnish, with only the addition of either A? from the major scale or G# from the minor, a full chromatic chord for one major and one minor chord, and a secondary chromatic chord for one more in each mode. [Scientific Basis and Build of Music, page 52]
The dominant seventh, G, B, D, F, a 4-note chord,1 only requires that the root G be made sharp, which will make G#-B a minor third agreeably with the structure of the other two intervals, B-D and E-F. The chromatic chord only differs from the dominant seventh in that it is wholly of minor thirds. There are four notes in a chromatic chord, but only three of them move by semitonic progression to a tonic chord. When these three notes thus move to a major chord, one is upward to the root, a second downward to the top, and the third downward also to the middle. The relative minor being a minor third below [Scientific Basis and Build of Music, page 52]
not mathematically identical, the genetic number of the last D, the top of the dominant major, being 27, and that of the first D, the root of the subdominant minor, being 26 2/3. Well, in the triplets of the minor we have minor thirds below their middles, D-F, A-C, E-G. In the triplets of the major we have minor thirds above their middles, A-C, E-G, B-D. But here between the triplets of the two modes we have a triplet which has minor third both below and above its middle note, two minor thirds and nothing else, B-D-F. Here, then, the Diatonic progression chords presents us with a 3-note Chromatic chord, and marchals us the way that we must go to find [Scientific Basis and Build of Music, page 54]
But, as the subdominant sixth and dominant seventh suggest that the chromatic chord should be a 4-note chord, we must find out how Nature completes this diatonic chromatic triad and makes it a 4-note chord, and that according to its own intrinsic character as of minor thirds. Nature has always a rationale in her operations which it is ever delightful to discover. Wedged in between the minor dominant and the major subdominant, this triad, B D F, has already B, the top of the dominant minor, for its root; and F, the root of the subdominant major, for its top; and its middle is the mysterious D which, in its two positions as root of the minor subdominant and top of the major dominant, stands at the two extremes of the whole twofold diatonic key, bounding and embracing all; and which in its two degrees as D26 2/3 and D27 claims kindred with both minor and major modes of the twofold key system. Surely this Janus-faced D, looking this way toward the minor and that way to the major, seems to say, "the complement of this chord, of which I am the heart, is not far to seek nor hard to find on either side." It has already B in common with the minor dominant; the very next step is to the middle of this chord, G. Roots and tops of chords may not be altered, but middles may with impunity be flattened or sharpened as occasion may require. No two of them in succession in the chord-scale have the same structure; the chromatic triad, in claiming this middle, claims it sharpened, for it must have [Scientific Basis and Build of Music, page 54]
a minor third. So by adding the middle of the minor dominant, G, but made G#, that the third so produced may be a minor third, according to the nature of the chromatic chords, we have on this minor side of the chord G#, B, D, F, which we may call its minor form, inasmuch as the semitone of its second minor third is the one, B-C, which genetically arises in the minor genesis; and inasmuch as it has also received its supplemental G# from the minor dominant. How shall we find its complement on the other side? We have seen that D, the Janus-faced center of this triad, B, D, F, looks, as D27, toward the major also; it has already F in common with the major subdominant. The very next step is to the middle of this chord, A. Middles, we have just seen, are ever ready to accommodate themselves; and this minor third triad claims that A be flattened, for on this side also, though its major side, it must have a minor third; so by adding the middle of the major subdominant, A, but made A?, according to the nature of chromatic intervals, that this F-A? also may be a minor third; and now we have it as B, D, F, A?, which we may call its major form, inasmuch as the semitone of its minor third, E-F, is the one which genetically arises in the major genesis, and inasmuch as it has now received its supplemental A? from the major subdominant. This, then, is the chromatic chord in its native place, and in its native constitution; a 4-note chord, wholly of the minor thirds. It will be observed that it has now, in its two forms, divided the octave into minor thirds - 4 minor thirds, so it is very much at home anywhere in the octave; indeed it is at home everywhere - G#, B, D, F, A?. And as every diatonic common chord in music is constituted of materials found in the octave of notes, it cannot be far from a chromatic chord in some one of its forms. [Scientific Basis and Build of Music, page 55]
We have already seen that this new compound chord, the chromatic, like the dominant seventh and subdominant sixth, is a 4-note chord, and, like them, made up of minor thirds - they mostly so, this wholly so; and we have seen that this compound chord embraces the whole octave, cutting it into minor thirds -
And now we shall also see the chromatic chord system cutting the octave into semitones. If we follow this chromatic chord system out, we shall have the octave [Scientific Basis and Build of Music, page 55]
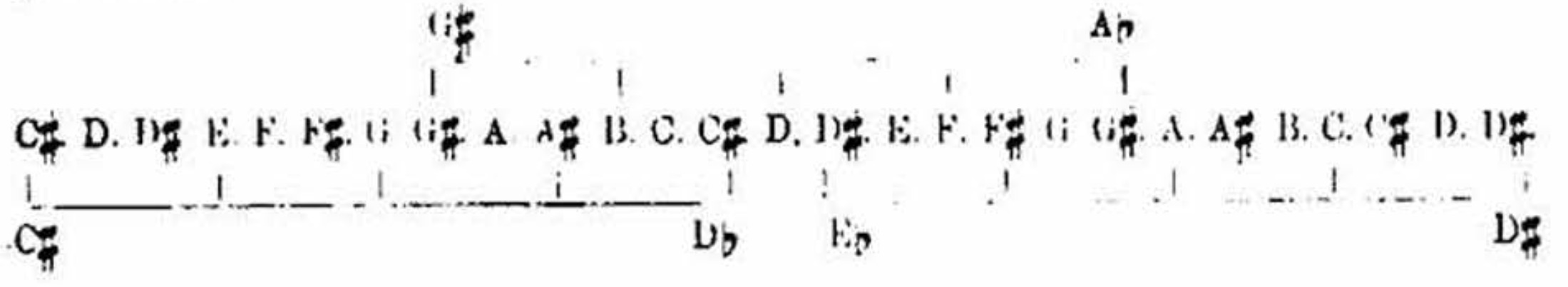
In the above line it will be readily observed that these three chromatic chords, having each of their intervals a minor third, involve, as necessary elements of their build, every one of the twelve semitones at one point or another of the line. This is a second witness to the legitimacy of the chromatic scale of twelve semitones. We have our first witness to the same in the evolution of the semitones progressively in the course of the modulations by which, in growth-like continuity, Nature links the successive keys; whether developed upward, as is the natural way of the majors; or downward, as in the natural way of the minors; or half upward and half downward, which is an expedient in order to simplify the signatures. In whichever direction the modulation is effected, one note is always divided, and must, true to Nature, be signified by placing a sharp or a ?, as the case may be, to the 4-comma altered interval, and this always leaves a 5-comma interval to occupy the place to which Nature has assigned such interval in the original scale. When this operation has been twelve times performed, we have the chromatic scale of twelve semitones. Thus by two witnesses the thing is established. By further examination of these chromatic chords we find other interesting features beside their witness to the twelve semitones of the octave. [Scientific Basis and Build of Music, page 56]
By taking four minor thirds upward from G# or downward from A?, we have the first chromatic chord in its twofold form. Its central note is D, the top of the dominant major, and the root of the subdominant minor, being its own dual, that is to say, its minor birth being dual to its major birth.1 On the keyboard it has the same order of keys above it and below it; this dual D [Scientific Basis and Build of Music, page 56]
being also the center of the diatonic triplet, B, D, F, which is the diatonic germ of the chromatic system. Four minor thirds upward or downward from C# we have a second chromatic chord, its central note being G. The dual1 of C# is E?; and there is the same order of keys on the keyboard2 below C# as there is above E?. Four minor thirds from E? upward or downward forms a third chromatic chord, the central note of which is A. The dual A, the center of the third chromatic, is G, the center of the second; and these two notes, by their duality, and by the duality of the two chords throughout, balance each other exactly on the keyboard on either side of the first chromatic chord, which contains all its own duals, and by this self-duality sits in the center, like the tonic chord among the diatonic three. [Scientific Basis and Build of Music, page 57]
contrast. In the fifth, the ratio being 2:3, the excess of 3 above 2 is 1; this 1 bears a simple relation to both the notes which awaken it. The grave harmonic in this case gives the octave below the lower of the two sounds; 1 is an octave below 2. This is the simplest relation "a third sound" can have to the two which awaken it, and that is why the fifth has the smallest possible degree of contrast. The octave, the fifth, and the fourth may be reckoned as simple ratios; the major and minor thirds and their inversions as moderately complex; the second, which has the ratio of 9:10, and the major fourth F to B and its inversion, are very complex. [Scientific Basis and Build of Music, page 61]
less variety of effect than we find in the diatonic chords; for although these chords may appear with their notes diversely named, there are still only the three. On account of their cosmopolitan character they need, and they have, no compounding with anything else. They are themselves at home everywhere; like a universal joint, they can turn any way, and affiliate in all directions. Being 4-note chords, and all of minor thirds, their effect is always minor, and they fall with loving softness to the diatonic chords to which they resolve. How this chord in its germ is found in the diatonic chord-scale; how it becomes a 4-note chord of minor thirds; how it variously resolves, each one of the three, in three manners with 24 tonic chords - all this is so fully set forth in the pre-note and treatise on the chromatic chord that it need not be more discussed in this place. See also Plates XVI., XVII., XVIII., XIX., and XX. [Scientific Basis and Build of Music, page 73]
The root of the subdominant is F, in the key of C major; and the top of the dominant is D. The difference between these two notes at the top and bottom of the chord-scale, is the quantity which two octaves is more than three fifths; it is the ratio of 27 to 30, a comma less than the minor third whose ratio is 5 to 6. [Scientific Basis and Build of Music, page 76]
G# as it occurs in the scales of A, E, and B major, and A? as it occurs in the scales of F and B? minor, are only distant the apotome minor, and are well represented by one key of the piano. It is only G# as it occurs in the scale of F six sharps major, and A? as it occurs in the scale of E six flats minor, that is not represented on the piano. These two extreme notes F# and E? minor are at the distance of fifteenth fifths and a minor third from each other. This supplies notes for 13 major and 13 minor mathematical scales; but as this is not required for our musical world of twelve scales, so these far-distant G# and A? are not required. The piano is only responsible for the amount of tempering which twelve fifths require, and that is never more than one comma and the apotome minor. [Scientific Basis and Build of Music, page 80]
Having found the framework of the major scale by multiplying F1 three times by 3, find the framework of the minor by dividing three times by 3. But what shall we divide? Well, F1 is the unbegotten of the 25 notes of the great genetic scale; B45 is the last-born of the same scale. We multiply upward from F1 for the major; divide downward from B45 for the minor. Again, B45 is the middle of the top chord of the major system, a minor third below D, the top of that chord, and the top of the whole major chord-scale, so B is the relative minor to it. Now since the minor is to be seen as the INVERSE of the major, the whole process must be inverse. Divide instead of multiply! Divide from the top chord instead of multiply from the bottom chord. Divide from the top of the minor dominant instead of multiply from the root of the major subdominant. This will give the framework of the minor system, B45/3 = E15/3 = A5/3 = D1 2/3. But as 1 2/3 is not easily compared with D27 of the major, take a higher octave of B and divide from it. Two times B45 is B90, and two times B90 is B180, and two times B180 is B360, the number of the degrees of a circle, and two times B360 is B720; all these are simply octaves of B, and do not in the least alter the character of that note; now B720/3 is = E240/3 = A80/3 = D26 2/3. And now comparing D27 found from F1, and D26 2/3 found from B720, we see that while E240 is the same both ways, and also A80, yet D26 2/3 is a comma lower than D27. This is the note which is the center of the dual system, and it is itself a dual note befittingly. [Scientific Basis and Build of Music, page 81]
Here on the keyboard we see, nearest to the front, the great 3-times-3 chord of the full genesis of the scale from F1 to F64. When this chord is struck by the notched lath represented in front of the keyboard, the whole harmony of the key is heard at once. Behind this great chord are placed, to the left the subdominant, tonic, and dominant chords of the minor. D F A, A E C, E G B; and to the right the subdominant, tonic, and dominant chords of the major, F A C, C E G, G B D. When the notched lath is shifted from F to D, the minor third below F, and the 3-times-3 minor is struck down in the same way as the major, the whole harmony is heard; and the complete contrast of effect between major and minor harmony can be fully pronounced to the ear by this means. Behind these six diatonic chords, major and minor, on the part of the keyboard nearest to the black keys, are the three chromatic chords in their four-foldness, in both major and minor form. The center one shows the diatonic germ of the chromatic chord, with its supplement of G# on the one hand completing its minor form, and its supplement of A? on the other hand completing its major form. A great deal of teaching may be illustrated by this plate.
This plate is a representation of the area of a scale; the major scale, when viewed with the large hemisphere, lowest; the minor when viewed the reverse way. It is here pictorially shown that major and minor does not mean larger and smaller, for both modes occupy the same area, and have in their structure the same intervals, though standing in a different order. It is this difference in structural arrangement of the intervals which characterizes the one as masculine and the other as feminine, which are much preferable to the major and minor as distinctive names for the two modes. Each scale, in both its modes, has three Fifths - subdominant, tonic, and dominant. The middle fifth is the tonic, and its lowest note the key-note of the scale, or of any composition written in this scale. The 53 commas of the Octave are variously allotted in its seven notes - 3 of them have 9 commas, 2 have 8, and 2 have 5. The area of the scale, however, has much more than the octave; it is two octaves, all save the minor third D-F, and has 93 commas. This is the area alike of masculine and feminine modes. The two modes are here shown as directly related, as we might figuratively say, in their marriage relation. The law of Duality, which always emerges when the two modes are seen in their relationship, is here illustrated, and the dual notes are indicated by oblique lines across the pairs. [Scientific Basis and Build of Music, page 106]
In the festoons of ellipses the signatures are given in the usual conventional way, the major F having one flat and minor E having one sharp. The major and minor keys start from these respective points, and each successive semitone is made a new keynote of a major and a minor respectively; and each ellipse in the festoons having the key shown in its two forms; for example, in the major F, one flat, or E#, eleven sharps; in the minor E, one sharp, or F?, eleven flats. Thus is seen all the various ways that notes may be named. The four minor thirds which divide the octave may be followed from an ellipse by the curved lines on which the ellipses are hung; and these four always constitute a chromatic chord. [Scientific Basis and Build of Music, page 115]
Fig. 1. - This figure shows the major and minor measured in commas and placed directly as they stand related, major and relative minor, the minor being set a minor third lower than the major. The interval between C and E in the minor is an 8-and-9-comma interval; between C and E in the major it is a 9-and-8-comma one. This difference arises from the minor D being a comma lower than the major D. In all the other intervals minor and major are the same. [Scientific Basis and Build of Music, page 120]
See Also
05 - The Melodic Relations of the sounds of the Common Scale
ATOMIC THIRD SUBDIVISION
celestial thirds
clustered thirds
diatonic third
enharmonic third
female
feminine
Figure 11.01 - Octave composed of Equal Thirds and Triads
Interval
introductory third
Keplers Third Law
Major Third
minor
Mother
negative thirds
Part 14 - Keelys Mysterious Thirds Sixths and Ninths
Prime Third
sympathetic thirds
Table 1 - Relations of Thirds
Table 1 - Relations of Thirds see also
Table 14.01 - All phrases in HyperVibes containing the term thirds
Table 14.02 - Neutral Thirds - Energy Radiates from Center - Force Contracts to Center
third
third element
Third Law of Thermodynamics
third octave
third subdivision
thirds
12.07 - Keelys Thirds Sixths and Ninths
13.28 - Differentiating Thirds
14.04 - Thirds as Currents
14.05 - Thirds as Differentiations
14.07 - Thirds in Magnetic Action
14.08 - Thirds as Assimilatives
14.10 - Thirds as Ratios within a Whole
14.28 - Thirds as Polar and Depolar Parameters
16.08 - Polar Link in Thirds
7.12 - Third
