Keely "Recently some questions, propounded to Mr. Keely by a scientist, elicited answers which the man of science admitted were clear and definite, but no physicist could accept Keely's assertion that incalculable amounts of latent force exist in the molecular space, for the simple reason that science asserts that molecular aggregation is attended with dissipation of energy instead of its absorption. The questions asked were:-
I. "In disintegrating water, how many foot-pounds of energy have you to expend in order or produce or induce the vibratory energy in your acoustical apparatus?"
Answer.- "No foot-pounds at all. The force necessary to excite disintegration when the instrument is sensitized, both in sensitization and development, would not be sufficient to wind up a watch."
II. "What is the amount of energy that you get out of that initial amount of water, say twelve drops, when decomposed into ether?"
Answer.- "From twelve drops of water a force can be developed that will fill a chamber of seven pint volume no less than six times with a pressure of ten tons to the square inch."
III. "In other words, if you put so many pounds of energy into vibratory motion, how many foot-pounds do you get out of this?"
Answer.- "All molecular masses of metal represent in their interstitial molecular spaces incalculable amounts of latent force, which if awakened and brought into intense vibratory action by the medium of sympathetic liberation, would result in thousands of billions more power in foot-pounds than that necessary to awaken it. The resultant development of any and all forces is only accomplished by conditions that awaken the latent energy they have carried with them during molecular aggregation. If the latent force that exists in a pound of water could be sympathetically evolved or liberated up to the seventh subdivision or compound interetheric, and could be stored free of rotation, it would be in my estimation sufficient to run the power of the world for a century." [Vibratory Physics - True Science]
Ramsay
Twelve divisions in the Octave serve all the purposes of music. This is the master-stroke of Nature in putting so much into seemingly so little. Twelve is the most genial of all numbers; it is nature's representative of the social order in music. It is the manifold divisibility of twelve which makes the chromatic system in music possible. The equalized scale of twelve semitones in the octave and the chromatic system of music are indissolubly connected. With this the scale of mathematical intonation has neither part nor lot.
The life-force of the notes from the law of position gives them a versatility which they could never have had from fixed ratios, however numerous. If the interval of the octave be excepted, there are no two notes together in a chord, nor succeeding each other in the octave scale, having the same amount of specific levity or gravity; consequently each note has an expression and [Scientific Basis and Build of Music, page 35]
The twelve semitones being the practical fulfillment of the ratios when the life-force of the notes is considered, the great masters had the ratios in their most workable form invested in their key-boards, and this along with the musical ear was the sure word of prophecy to them.1 In their great works they have thus been enabled to develop the science of music, and to express it in the language of its art. [Scientific Basis and Build of Music, page 36]
that Nature has done so.1 And in every new key into which we modulate Nature performs the same operation, till in the course of the twelve scales she has cut every greater note into two, and made the notes of the scale into twelve instead of seven. These we, as a matter of convenience, call semitones; though they are really as much tones as are the small intervals which Nature gave us in the Genesis of the first scale between B-C and E-F. She only repeats the operation for every new key which she had performed at the very first. It is a new key, indeed, but exactly like the first. The 5 and 9 commas interval between E and G becomes a 9 and 5 comma interval; and this Nature does by the rule which rests in the ear, and is uttered in the obedient voice, and not by any mathematical authority from without. She cuts the 9-comma step F to G into two, and leaving 5 commas as the last interval of the new key of G, precisely as she had made 5 commas between B and C as the last interval of the key of C, she adds the other 4 commas to the 5-comma step E to F, which makes this second-last step a 9-comma step, precisely as she had made it in the key of C.2 [Scientific Basis and Build of Music, page 48]
divided into twelve semitones, thus - G#, A, A#, B, C, C#, D, D#, E, F, F#, G, G#. This is the operation which has stood done in our keyboards for many generations - [Scientific Basis and Build of Music, page 56]
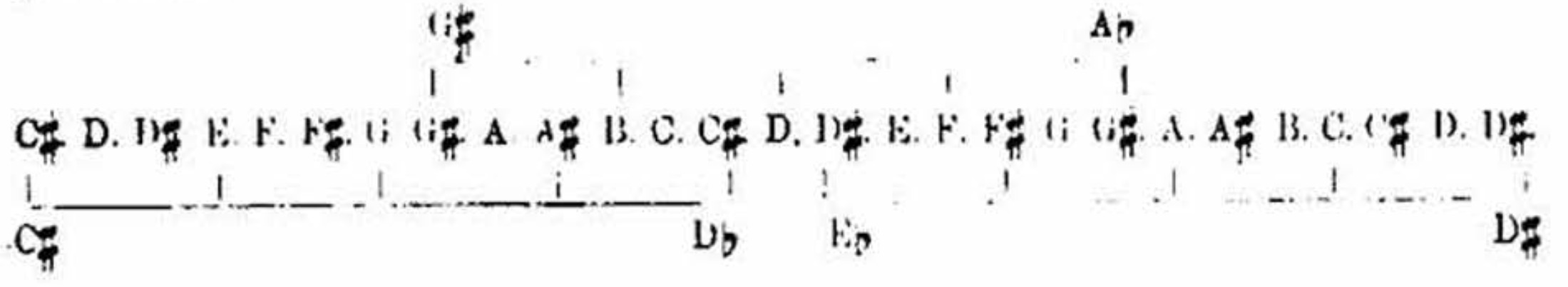
In the above line it will be readily observed that these three chromatic chords, having each of their intervals a minor third, involve, as necessary elements of their build, every one of the twelve semitones at one point or another of the line. This is a second witness to the legitimacy of the chromatic scale of twelve semitones. We have our first witness to the same in the evolution of the semitones progressively in the course of the modulations by which, in growth-like continuity, Nature links the successive keys; whether developed upward, as is the natural way of the majors; or downward, as in the natural way of the minors; or half upward and half downward, which is an expedient in order to simplify the signatures. In whichever direction the modulation is effected, one note is always divided, and must, true to Nature, be signified by placing a sharp or a ?, as the case may be, to the 4-comma altered interval, and this always leaves a 5-comma interval to occupy the place to which Nature has assigned such interval in the original scale. When this operation has been twelve times performed, we have the chromatic scale of twelve semitones. Thus by two witnesses the thing is established. By further examination of these chromatic chords we find other interesting features beside their witness to the twelve semitones of the octave. [Scientific Basis and Build of Music, page 56]
Had D. C. Ramsay lived to weld together his findings in musical science, there would have been fewer, it any, of these desultory notes. The Editor, in endeavoring to arrange his materials so as to give sequence and fullness to them as far as possible, has thought it better to allow these fragments to appear thus as Brevia, than to intertwine them with even the kindred studies of another to any great extent, feeling assured that the light Ramsay has let in upon musical science will lead the way probably to further findings, and certainly to more perfect settings of what, being found, is here set forth in a first edition of his works. [Scientific Basis and Build of Music, page 74]
There are very few things in music which have not change written upon them. TWELVE and THREE, however, are stable. There is nothing that will disturb the propriety of the circle of twelve fifths, as in the tempered system of music; for, although the mathematical-intonation indulges in thirteen keys, the thirteenth is simply the first of a new cycle of twelve. The working model of three fifths is that which possesses musical life-powers; and these life-powers go with it wherever it goes, and they go with nothing else. [Scientific Basis and Build of Music, page 74]
The difference between B# and C? is the apotome minor - a very small difference - and this can only occur in the mathematical scales. In tempered scales, such as are played on the piano, one key serves equally well for both. Although seven sharps may be employed, seven black keys are necessary. As F# and G? have the same relation to each other as B# and C?, and as B# does not require a black key but is found on a white one, so all the semitonic necessities for twelve tempered scales are fully supplied by 5 black keys, since the white keys are as much semitonic as the black ones. [Scientific Basis and Build of Music, page 80]
The reason why there are 13 mathematical scales is that G? and F# are written separately as two scales, although the one is only a comma and the apotome minor higher than the other, while in the regular succession of scales the one is always 5 notes higher than the other; so this G? is an anomaly among scales, unless viewed as the first of a second cycle of keys, which it really is; and all the notes of all the scales of this second cycle are equally a comma and the apotome higher than the notes of the first cycle; and when followed out we find that a third cycle is raised just as much higher than the second as the second is higher than the first; and what is true of these majors may be simply repeated as to the D# and E? of the minors, and the new cycle so begun, and all successive minor cycles. Twelve and not thirteen is the natural number for the mathematical scales, which go on in a spiral line, as truly as for the tempered scales, which close as a circle at this point. [Scientific Basis and Build of Music, page 89]
"Dividing the octave into twelve semitones is a near approach to the mathematical quantities, and this saves the musical artist from errors in tone - at least to any extent; but it does not save from errors in judgment. In the case of G#, for example, not one of the reasons given for the use of the sharp seventh in the minor scale is a correct one. A touch of nature makes the world akin, and a touch of the Law of Duality balances everything in music." [Scientific Basis and Build of Music, page 99]
save the octave, and made them into one, so that in its proximate meetings during its period it seems composed of the ratio 2:3 twelve times, and 3:4 seven times; twelve times 2 and seven times 3 are 45; twelve times 3 and seven times 4 are 64. This long period of 45 to 64 by its proximate meetings divided itself into 19 short periods, and oscillates between the ratios of 2:3 and 3:4 without ever being exactly the one or the other; the difference being always a very small ratio, and the excess of the one being always the deficiency of the other. This fifth, B to F, has been misnamed an "imperfect fifth." When these two notes in the ratio of 45:64 are heard together, the oscillating proximately within it of the two simple ratios gives this fifth a trembling mysterious sound. [Scientific Basis and Build of Music,page 106]
When Leonhard Euler, the distinguished mathematician of the eighteenth century, wrote his essay on a New Theory of Music, Fuss remarks - "It has no great success, as it contained too much geometry for musicians, and too much music for geometers." There was a reason which Fuss was not seemingly able to observe, namely, that while it had hold of some very precious musical truth it also put forth some error, and error is always a hindrance to true progress. Euler did good service, however. In his letters to a German Princess on his theory of music he showed the true use of the mathematical primes 2, 3, and 5, but debarred the use of 7, saying, "Were we to introduce the number 7, the tones of an octave would be increased." It was wise in the great mathematician to hold his hand from adding other notes. It is always dangerous to offer strange fire on the altar. He very clearly set forth that while 2 has an unlimited use in producing Octaves, 3 must be limited to its use 3 times in producing Fifths. This was right, for in producing a fourth Fifth it is not a Fifth for the scale. But Euler erred in attempting to generate the semitonic scale of 12 notes by the use of the power of 5 a second time on the original materials. It produces F# right enough; for D27 by 5 gives 135, which is the number for F#. D27 is the note by which F# is produced, because D is right for this process in its unaltered condition. But when Euler proceeds further to use the prime 5 on the middles, A, E, and B, and F#, in their original and unaltered state, he quite errs, and produces all the sharpened notes too low. C# for the key of D is not got by applying 5 to A40, as it is in its birthplace; A40 has already been altered for the key of G by a comma, and is A40 1/2 before it is used for producing its third; it is A40 1/2 that, multiplied by 5, gives C#202 1/2, not C200, as Euler makes C#. Things are in the same condition with E before G# is wanted for the key of A. G# is found by 5 applied to E; not E in its original and unaltered state, E30; but as already raised a comma for the key of D, E30 3/8; so G# is not 300, as Euler has it, but 303 3/4. Euler next, by the same erroneous methods, proceeds to generate D# from B45, its birthplace number; but before D# is wanted for the key of E, B has been raised a comma, and is no longer B45, but B45 9/16, and this multiplied by 5 gives D#227 13/16, not D225, as Euler gives it. The last semitone which he generates to complete his 12 semitones is B?; that is A#, properly speaking, for this series, and he generates it from F#135; but this already altered note, before A# is wanted for the key of B, has been again raised a comma [Scientific Basis and Build of Music, page 107]
One purpose of this plate is to show that twelve times the interval of a fifth divides the octave into twelve semitones; and each of these twelve notes is the first note of a major and a minor scale. When the same note has two names, the one has sharps and the other has flats. The number of sharps and flats taken together is always twelve. In this plate will also be observed an exhibition of the omnipresence of the chromatic chords among the twice twelve scales. The staff in the center of the plate is also used as to show the whole 24 scales. Going from the major end, the winding line, advancing by fifths, goes through all the twelve keys notes; but in order to keep all within the staff, a double expedient is resorted to. Instead of starting from C0, the line starts from the subdominant F0, that is, one key lower, and then following the line we have C1, G2, etc., B6 proceeds to G? instead of F#, but the signature-number continues still to indicate as if the keys went on in sharps up to F12, where the winding line ends. Going from the minor end, the line starts from E0 instead of A0 - that is, it starts from the dominant of A0, or one key in advance. Then following the line we have B1, F#2, etc. When we come to D#5, we proceed to B? instead of A#6, but the signature-number continues as if still in sharps up [Scientific Basis and Build of Music, page 114]
The middle portion with the zigzag and perpendicular lines are the chromatic chords, as it were arpeggio'd. They are shown 5-fold, and have their major form from the right side, and their minor form from the left. In the column on the right they are seen in resolution, in their primary and fullest manner, with the 12 minors. The reason why there are 13 scales, though called the 12, is that F# is one scale and G? another on the major side; and D# and E? separated the same way on the minor side. Twelve, however, is the natural number for the mathematical scales as well as the tempered ones. But as the mathematical scales roll on in cycles, F# is mathematically the first of a new cycle, and all the notes of the scale of F# are a comma and the apotome minor higher than G?. And so also it is on the minor side, D# is a comma and the apotome higher than E?. These two thirteenth keys are therefore simply a repetition of the two first; a fourteenth would be a repetition of the second; and so on all through till a second cycle of twelve would be completed; and the thirteenth to it would be just the first of a third cycle a comma and the apotome minor higher than the second, and so on ad infinitum. In the tempered scales F# and G? on the major side are made one; and D# and E? on the minor side the same; and the circle of the twelve is closed. This is the explanation of the thirteen in any of the plates being called twelve. The perpendicular lines join identical notes with diverse names. The zigzag lines thread the rising Fifths which constitute the chromatic chords under diverse names, and these chords are then seen in stave-notation, or the major and minor sides opposites. The system of the Secondary and Tertiary manner of resolution might be shown in the same way, thus exhibiting 72 resolutions into Tonic chords. But the Chromatic chord can also be used to resolve to the Subdominant and Dominant chords of each of these 24 keys, which will exhibit 48 more chromatic resolutions; and resolving into the 48 chords in the primary, secondary, and tertiary manners, will make 144 resolutions, which with 72 above make 216 resolutions. These have been worked out by our author in the Common Notation, in a variety of positions and inversions, and may be published, perhaps, in a second edition of this work, or in a practical work by themselves. [Scientific Basis and Build of Music, page 115]
These two plates show the chromatic chord resolving into the twelve major and twelve minor tonic chords of the twenty-four scales. There seems to be twenty-five, but that arises from making G? and F# in the major two scales, whereas they are really only one; and the same in the minor series, E? and D# are really one scale. C in the major and A in the minor, which occur in the middle of the series, when both sharps and flats are employed in the signatures, are placed below and outside of the circular stave to give them prominence as the types of the scale; and the first chromatic chord is seen with them in its major and minor form, and its typical manner of resolving - the major form rising to the root, and falling to the top and middle; the minor form falling to the top, and rising to the root and middle. The signatures of the keys are given under the stave. [Scientific Basis and Build of Music, page 116]
with her irrevocable proportions to measure his scales for him. The stars at the C of the first scale and at the B# of the last show the coincidence of 12 fifths and 7 octaves. The number of B# is 3113 467/512; C24 multiplied 7 times by 2 brings us to the number 3072; these two notes in the tempered system are made one, and the unbroken horizon of the musical world of twelve twofold keys is created. The very small difference between these two pitches is so distributed in the 12 tempered scales that no single key of the 12 has much to bear in the loss of perfect intonation. [Scientific Basis and Build of Music, page 118]
Hughes
The eighteen tones of keyed instruments veering round and in musical clef below, the twelve seen that develope major keys
—The seven colours answer to the seven white notes
—The use of the two chasms, the key-note C and its root F rising from them
—A major key-note complete in itself, embracing the eighteen tones
—In the whole process of harmony there is limit, every key-note having its point of rest, and yet it is illimitable, . . . . . . . 22 [Harmonies of Tones and Colours, Table of Contents2 - Harmonies]
The twelve keys, their trinities, scales, and chords, rising seven times through seven octaves, each thirteenth note octave of the previous twelve and first of the rising twelve
—Descending, ascending reversed
—Keys mingled
—The Pendulograph alluded to, . . . 28 [Harmonies of Tones and Colours, Table of Contents2 - Harmonies]
The modulating gamut
—One series of the twelve keys meeting by fifths through seven octaves
—Keys not mingled
—A table of the key-notes and their trinities thus meeting
—The fourths not isolated
—The table of the twelve scales meeting by fifths
—The twelve keys, trinities, scales, and chords thus meeting are written in musical clef
—The twelve meeting through seven circles, each circle representing the eighteen tones
—The keys of C and G meeting, coloured
—Retrospection of the various major developments, . . . . 29 [Harmonies of Tones and Colours, Table of Contents3 - Harmonies]
The minor harmonies
—The eighteen tones repeated veering round, and in musical clef below, showing the twelve that develope minor harmonies
—The twelve minor key-notes as gained from the twelve major, . . . . . . . . . . 32 [Harmonies of Tones and Colours, Table of Contents3 - Harmonies]
If the laws which I shall endeavour to explain develope the twelve major harmonies, with each note in succession expanding its six tones from within itself; and if each of these is found to be a lower development, which leads the ear to a corresponding higher expansion of the twelve major key-notes, and the six tones of each ascending and descending in an unbroken sequence from any twelve consecutively, the thirteenth being the octave of the first, which commences a higher or a lower series; and if the twelve minor harmonies are also gained by the same laws from their twelve relative key-notes (the thirteenth again being octave): if, again, all other notes are shown to be but higher or lower repetitions of these twenty-four harmonies—may we not consider the problem as in some measure solved? especially as the harmonies proceed in geometric as well as harmonical ratio, and an accurate parallel can be traced between the development of notes and colours, which latter correspond with all the intricacies of harmonic sounds. [Harmonies of Tones and Colours, The Method of Development or Creation of Harmonies3, page 17]
The twelve which develope twelve major harmonies are written thus
the other six which are incapabable of developing major harmonies thus
without regard to musical time. The seven colours are shown to answer to the seven white notes, the other five being intermediate tones and colours. A flat marked to a note indicates that it is nearer to the tone or colour below; a sharp means that it is nearer to the tone or colour above. The notes and chasms are not written according to accurately measured degrees. [Harmonies of Tones and Colours, Diagram I - The Eighteen Tones of Keyed Instruments, page 22a]
In any series of twelve, the primaries of the two first key-notes repeat the secondaries of the two last of a lower series of twelve; and the two last secondaries of the twelve in development are sounded as the two first primaries of a higher series of twelve. The three series are thus linked into each other. [Harmonies of Tones and Colours, Combinations of dissonance, rests, page 24]
This diagram represents the two last major primaries of a series of 12; 12 of a higher series follow, and the two first of a still higher series: the secondaries are written below the primaries, the sharps or flats belonging to the different harmonies are written to each note. Each primary sounds the same tones as the secondaries of each third harmony below, but in a different order; and the double tones are altered sharp or flat as the harmonies require.
By reference to previous coloured notes it will be seen that all these agree. [Harmonies of Tones and Colours, The Two Last Major Primaries, page 24e]
The twelve key-notes, with the six notes of each as they veer round in trinities, are again written in musical clef, and the scales added. The key-note leads the scale, and, after striking the two next highest notes of the seven of the harmony, goes forward, with its four lowest, an octave higher. The seven of each harmony have been traced as the three lowest, thus meeting the three highest in three pairs, the fourth note being isolated. Notwithstanding the curious reversal of the three and four of the scale, the three lowest pair with the three highest, and the fourth with its octave. The four pairs are written at the end of each line, and it will be seen how exactly they all agree in their mode of development. Keys with sharps and keys with flats are all mingled in twelve successive notes. If we strike the twelve scales ascending as they follow each other, each thirteenth note being octave of the first note of the twelve that have developed, and first of the rising series, the seventh time the scales gradually rise into the higher series of seven octaves beyond the power of the instrument. Descending is ascending reversed. After the seven and octave of a scale have been sounded ascending, the ear seems to lead to the descending; but ten notes of any scale may be struck without the necessity of modulation; at the seventh note we find that the eleventh note in the progression of harmonics rises to meet the seventh. For instance, B, the seventh note in the scale of C, must have F#. This point will be fully entered into when examining the meeting of fifths. To trace the scale of C veering round as an example for all, we may begin with C in Diagram II., and go forward with F, G, A, and B an octave higher. If the twelve scales were traced veering round, they would be found to correspond with the twelve as written in musical clef. [Harmonies of Tones and Colours, Diagram IV - The Development of the Twelve Major Scales, page 26a]
ON a keyed instrument only twelve are major key-notes, but as the double tones C#-D? and F#-G? are roots, there are fourteen different chords. The fourteen that are roots are written in musical clef. As an example of the major chords in the different keys, we may examine those in the key of C. A major fifth includes five out of the seven of its key; with the third or central note it is the threefold chord, or fourfold when the octave note is added. Including the silent key-notes, a threefold chord embraces eight, or, counting the double tones, not including E#, eleven. The first and second chords of the seven of the harmony are perfect major chords in the key of C; the central note of the third chord, being #C-?D, is a discord. The first pair of fifths in the scale, with its central note, is a chord of the key; if we include the octave, the last pair of fifths, with its central note, is the same chord an octave higher than the lowest chord of the seven. Of the chords written in musical clef of the twelve keys, the octave chord is only written to C, the seven of each having two chords and the scale one, thirty-six in all, or forty-eight if the octave chords are added. Notice how the chords of each seven and the chord of its scale are altered. [Harmonies of Tones and Colours, Diagram V - The Chords of the Twelve Major Keys, page 27a]
THE twelve keys have been traced following each other seven times through seven octaves, the keys mingled, the thirteenth note being the octave, and becoming first of each rising twelve. Thus developing, the seven notes of each eighth key were complementary pairs, with the seven notes of each eighth key below, and one series of the twelve keys may be traced, all meeting in succession, not mingled. When the notes not required for each of the twelve thus meeting are kept under, the eighths of the twelve all meet by fifths, and as before, in succession, each key increases by one sharp, the keys with flats following, each decreasing by one flat; after this, the octave of the first C would follow and begin a higher series. It is most interesting to trace the fourths, no longer isolated, but meeting each other, having risen through the progression of the keys to higher harmonies. In the seven of C, B is the isolated fourth, meeting F#, the isolated fourth in the key of G, and so on. Each ascending key-note becomes the root of the fifth key-note higher; thus C becomes the root of G, &c. [Harmonies of Tones and Colours, Diagram VII - The Modulating Gamut of the Twelve Keys1, page 29]
Round the circle the eighteen tones of keyed instruments are shown; the twelve developing perfect minor keys are written thus
, the seven white-keyed notes are coloured, the intermediate tones left uncoloured. [Harmonies of Tones and Colours, Diagram VIII - On the Development of the Twelve Minor Harmonies, page 32]
Below the circular diagram are seen in musical clef the twelve minor key-notes, as gained from the majors. There is only one meeting of the same note in the seven of every major harmony. All the twelve follow the same plan; the lowest note of the seven of C is F, the highest note of the seven is E. The lowest tone sounded by E and the highest tone sounded by F is the same, A—leading the ear from C to its relative minor A. [Harmonies of Tones and Colours, The Minor Harmonies, page 33a]
THE same laws are followed here as in the development of the major scales. In that of A, F, the sixth note, has risen to F#, in order to meet B, which has previously sounded. In descending, the seventh note, B, falls to B?, in order to meet F, which has also previously sounded. The notes, ascending or descending, always follow the harmony of their key-note, except when rising higher or falling lower to meet in fifths. We may here trace the twelve, the ascending scale sounding the fifth harmony higher than its key-note, and, in descending, sounding the fifth lower harmony. The four pairs of each scale are written at the end of the lines. If we strike the twelve scales as they follow in succession, the thirteenth note being the octave of the first, and leader of a higher twelve; having gained them six times, at the seventh they gradually rise (though beyond the power of a keyed instrument) into the higher series of seven octaves, and again, in descending, they fall lower, and are linked into the lower series of seven octaves. Nine notes of any ascending minor scale may be struck without the necessity of modulating beyond the fifth harmony. For example, in the scale of A, its tenth note, C#, rises to meet the sixth note, which has previously sounded. In descending, E?, the eleventh note, meets B?, the seventh note, which has previously sounded. The scale of A may be traced veering round by reference to Diagram IX., beginning with A, and carrying the four lowest notes an octave higher, F rising to F# in ascending, B falling to B? in descending. [Harmonies of Tones and Colours, Diagram XI - The Twelve Minor Keynotes with the Six Note of Each, page 36a]
ALTHOUGH only twelve notes of a keyed instrument develope perfect minor harmonics, there are fifteen different chords, the double tones D#-E?, E#-F?, A#-B? all sounding as roots. The fifteen roots are written in musical clef. A major and a minor fifth embrace the same number of key-notes, but the division into threefold chords is different. In counting the twelve, a major fifth has four below the third note of its harmony, and three above it; a minor fifth has three below the third note of its harmony, and four above it. A major seventh includes twelve key-notes, a minor seventh only eleven. As an example of the minor chords in the different keys, we may first examine those in the key of A, written in musical clef. The seven of its harmony have two threefold chords, and two of its ascending scale. If we include the octave note, the highest chord of the descending scale is a repetition (sounding an octave higher) of the lowest chord of the seven in its harmony, and the second chord of the descending scale is a repetition of the first chord of its ascending scale. These two repetition chords are only written to the key of A: the chords of the other eleven keys will all be found exactly to agree with those of A in their mode of development. We may again remark on the beautiful effect which would result if the colours of the minor chords could be seen, with the tones, as they develope. [Harmonies of Tones and Colours, Diagram XII - The Chords of the Twelve Minor Keys, page 37a]
IF we strike the twelve as written in musical clef, beginning with the lowest A in the bass clef, each key-note, with its trinities, scale, and chords, sounds three harmonics. We may follow with the twelve keys as they rise, and descend by following the keys upwards as written in musical clef, each key falling lower. [Harmonies of Tones and Colours, Diagram XIII - The Twelve Keynotes with Their Trinities, page 38a]
Let us first examine the meeting of the key-notes and their trinities in musical clef; the isolated fourths rising through the progression of the twelve now meet, seven and seven pairing. We must notice how closely they are linked into each other, the three highest notes of the lower seven being the three lowest of the higher seven an octave higher, and the four lowest becoming the four highest an octave higher; we descend by following the keys as written in musical clef upwards. [Harmonies of Tones and Colours, Diagram XIV - The Modulating Gamut of the Twelve Minor Keys by Fifths1, page 39]
Lastly, we trace the twelve ascending by fifths as they veer round through the seven circles, each circle representing the eighteen tones, beginning with A in the innermost circle. A becomes the root of E, E of B, and so on. In descending, we begin with A in the outermost circle, though it is in fact the commencement of a higher series which we cannot strike. D, its root, becomes the fifth key-note lower, and so on. The keys of A and E are coloured, to show the result of the minor harmonies meeting by fifths. [Harmonies of Tones and Colours, Diagram XIV - The Modulating Gamut of the Twelve Minor Keys by Fifths3, page 41a]
TO recapitulate from the beginning, observe, firstly, the twelve major key-notes as they have developed from within themselves in succession, six tones in trinities seven times through seven octaves, each thirteenth note being the octave of the first note of the twelve that have developed, and being also the first of the higher series. We may retrace all as still sounding their tones, the key-notes leading the ear to the six notes of each harmony, the keys with sharps and those with flats being mingled. The ascending and descending scales always agree in their harmonies with the key-notes and their trinities. [Harmonies of Tones and Colours, Diagram XV - The Twelve Major and the Twelve Minor Keys, page 42a]
Thirdly, the twelve minor keys as they develope in succession seven times through seven octaves, always sounding their major harmony in trinities, and, as with the majors, each thirteenth note being the octave of the first note of the twelve, and first of the following series, the keys all mingled. [Harmonies of Tones and Colours, Diagram XV - The Twelve Major and the Twelve Minor Keys, page 42a]
The Minor Gamut modulating in the meeting of fifths through seven octaves. We may here trace the twelve, each fifth note becoming the higher key-note. But the sixth and seventh notes of the scale are discords. For example, in the key of A, the sixth note, F?, is a discord with the second note, B?; and the seventh note cannot be sounded as G# falling into the eighth, without being a discord with the third note, C?. No octave can be sounded in the Minor Scale, as it has risen into the fifth higher key of E. [Harmonies of Tones and Colours, The Minor Gamut Modulating in the Meeting of Fifths61, page 65]
THE MAGIC OF NUMBER 12
For example, 12^7 (12X12X12X12X12X12X12X12) is 35,831,808-feet, which is the Moon's circumference (measured in feet). So, 35,831,808 divided by 5,280 is 6,786.327237-miles. Interestingly, 6,786.327237 X 86,400 (the number of seconds in a day) equals 586,338,674.4-miles (the Earth's orbital circumference). What's magic about this is that the ancient Sumerians knew this 5000-years ago. [anon]
Cayce
17. (Q) Please explain the twelve names which represent the twelve tribes of the children of Israel.
(A) The same as the twelve gates, the twelve angels, the twelve ways, the twelve understandings; or the approach to ISRAEL the seeker - all seeking not then as the expression of self but as ONE in the Holy One!! [Cayce 281-37]
See Also
11.13 - Dominant Conditions are Mated Opposing Pairs as Fifths
circle of fifths
circle of twelve fifths
cycle of twelve
fifth
fifths of chords
meeting by fifths
meeting of fifths
Ramsay - PLATE XXII - Mathematical Table of the Twelve Major Scales and their relative Minors
Ramsay - The Closed System of the Twelve Keys
Ramsay - The Evolution of the Twelve Scales a thing of Life
Ramsay - The Three Fifths which constitute the Scale
series of twelve
system of twelve Fifths
table of the twelve scales meeting by fifths
The twelve keys meeting by fifths
The Twelve Scales Meeting by Fifths
three fifths
twelve fifths
twelve fruits
twelve keys
twelve major keys
twelve major scales
twelve minor keys
twelve minor scales
twelve scales
twice twelve-fold family of keys
