A half a tone, or an approximate half a tone, half step, some portion of a whole (interval) step.
Ramsay
"While vibrations are the sound-stuff, the protoplasm of notes, semitones are, as it were, the atoms of which music is composed. We may think and talk of quarter tones and commas, apotomes and skismas, and dots, but these have no place as intervals for the musical ear, nor any part in the compositions which so charm us of the great masters." [Scientific Basis and Build of Music, page 20]
Nature's own art, not man's device, enables us to realize and represent all the harmonic progressions that belong to music. It has been nature's self to the practical and inspired musician. By the division of the octave into twelve semitones, he is emancipated from the restrictions and jargon which arise from misapplied mathematics. The mathematicians say that such and such things are wrong; the great masters in music inspirationally do these very things. [Scientific Basis and Build of Music, page 33]
she is found to have produced the Chromatic scale of twelve semitones, derived from her own vital operations; so that there are no anomalies. It is a degradation of the mathematical primes to apply them to the getting of the semitones of the chromatic scale, as even Euler himself mistakenly does. The mathematical ratios lead the way in getting the notes of the diatonic scale, and that is all that is required of them. The true praise to the ratios is that they have constituted an organic structure with form and life-powers adapted for self-development. It would be little credit to the mother if the child required to be all its life-long pinned to her apron-strings. As the bird when developed so far leaves the shell, and is afterwards fully developed in new conditions; so the System of music when developed so far leaves the law of ratios, its mathematical shell, and is afterwards fully developed by other laws. Music has an inspirational as well as a mathematical basis, and when mathematicians do not recognize this they reckon without their host. [Scientific Basis and Build of Music, page 35]
The twelve semitones being the practical fulfillment of the ratios when the life-force of the notes is considered, the great masters had the ratios in their most workable form invested in their key-boards, and this along with the musical ear was the sure word of prophecy to them.1 In their great works they have thus been enabled to develop the science of music, and to express it in the language of its art. [Scientific Basis and Build of Music, page 36]
The Greeks most probably constructed their musical tetrachords in a symmetrical order in analogy with their sculpture, and showed the ear identical with the eye in its love of symmetry. With them, therefore, the Dorian mode would have a certain pre-eminence. Beginning this mode on D, without knowing the musical mystery that resides in D, they had two tetrachords with the semitones symmetrically in the middle in one mode; it was next possible for them to arrange in pairs, symmetrically, the other tetrachords.
[Scientific Basis and Build of Music, page 45]
It should not be supposed that this division of the notes into semitones, as we call them, is something invented by man; it is only something observed by him. The cutting of the notes into twelve semitones is Nature's own doing. She guides us to it in passing from one scale to another as she builds them up. When we pass, for example, from the key of C to the key of G, Nature divides one of the intervals into two nearly equal parts. This operation we mark by putting a # to F. We do not put the # to F to make it sharp, but to show [Scientific Basis and Build of Music, page 47]
that Nature has done so.1 And in every new key into which we modulate Nature performs the same operation, till in the course of the twelve scales she has cut every greater note into two, and made the notes of the scale into twelve instead of seven. These we, as a matter of convenience, call semitones; though they are really as much tones as are the small intervals which Nature gave us in the Genesis of the first scale between B-C and E-F. She only repeats the operation for every new key which she had performed at the very first. It is a new key, indeed, but exactly like the first. The 5 and 9 commas interval between E and G becomes a 9 and 5 comma interval; and this Nature does by the rule which rests in the ear, and is uttered in the obedient voice, and not by any mathematical authority from without. She cuts the 9-comma step F to G into two, and leaving 5 commas as the last interval of the new key of G, precisely as she had made 5 commas between B and C as the last interval of the key of C, she adds the other 4 commas to the 5-comma step E to F, which makes this second-last step a 9-comma step, precisely as she had made it in the key of C.2 [Scientific Basis and Build of Music, page 48]
There are two semitones in each system, B-C and E-F. But when the notes of the two systems are being generated simultaneously, the two semitonic intervals originate separately. While the major is generating the semitone E-F, the third and fourth of the major scale, the minor is generating the semitone B-C, the second and third of the minor scale. So E-F is the semitone which belongs genetically to the major, and B-C to the minor.1 These two semitones are the two roots of
THE CHROMATIC SYSTEM,
and they are found together in what has been called the "Minor Triad," and by other names, namely, B-D-F. [Scientific Basis and Build of Music, page 50]
The triplet B, D, F, has been called the imperfect triad, because in it the two diatonic semitones, B-C and E-F, and the two minor thirds which they constitute, come together in this so-called imperfect fifth. But instead of deserving any name indicating imperfection, this most interesting triad is the Diatonic germ of the chromatic chord, and of the chromatic system of chords. Place this triad to precede the tonic chord of the key of C major, and there are two semitonic progressions. Place it to precede the tonic chord of the key of F# major, and there are three semitonic progressions. Again, if we place it to precede the tonic chord of the key of A minor, there are two semitonic progressions; but make it precede the tonic chord of E? minor, and there are three semitonic progressions. This shows that the chromatic chord has its germ in, and its outgrowth from the so-called "natural notes," that is notes without flats or sharps, notes with white keys; and that these natural notes furnish, with only the addition of either A? from the major scale or G# from the minor, a full chromatic chord for one major and one minor chord, and a secondary chromatic chord for one more in each mode. [Scientific Basis and Build of Music, page 52]
a minor third. So by adding the middle of the minor dominant, G, but made G#, that the third so produced may be a minor third, according to the nature of the chromatic chords, we have on this minor side of the chord G#, B, D, F, which we may call its minor form, inasmuch as the semitone of its second minor third is the one, B-C, which genetically arises in the minor genesis; and inasmuch as it has also received its supplemental G# from the minor dominant. How shall we find its complement on the other side? We have seen that D, the Janus-faced center of this triad, B, D, F, looks, as D27, toward the major also; it has already F in common with the major subdominant. The very next step is to the middle of this chord, A. Middles, we have just seen, are ever ready to accommodate themselves; and this minor third triad claims that A be flattened, for on this side also, though its major side, it must have a minor third; so by adding the middle of the major subdominant, A, but made A?, according to the nature of chromatic intervals, that this F-A? also may be a minor third; and now we have it as B, D, F, A?, which we may call its major form, inasmuch as the semitone of its minor third, E-F, is the one which genetically arises in the major genesis, and inasmuch as it has now received its supplemental A? from the major subdominant. This, then, is the chromatic chord in its native place, and in its native constitution; a 4-note chord, wholly of the minor thirds. It will be observed that it has now, in its two forms, divided the octave into minor thirds - 4 minor thirds, so it is very much at home anywhere in the octave; indeed it is at home everywhere - G#, B, D, F, A?. And as every diatonic common chord in music is constituted of materials found in the octave of notes, it cannot be far from a chromatic chord in some one of its forms. [Scientific Basis and Build of Music, page 55]
We have already seen that this new compound chord, the chromatic, like the dominant seventh and subdominant sixth, is a 4-note chord, and, like them, made up of minor thirds - they mostly so, this wholly so; and we have seen that this compound chord embraces the whole octave, cutting it into minor thirds -
And now we shall also see the chromatic chord system cutting the octave into semitones. If we follow this chromatic chord system out, we shall have the octave [Scientific Basis and Build of Music, page 55]
divided into twelve semitones, thus - G#, A, A#, B, C, C#, D, D#, E, F, F#, G, G#. This is the operation which has stood done in our keyboards for many generations - [Scientific Basis and Build of Music, page 56]
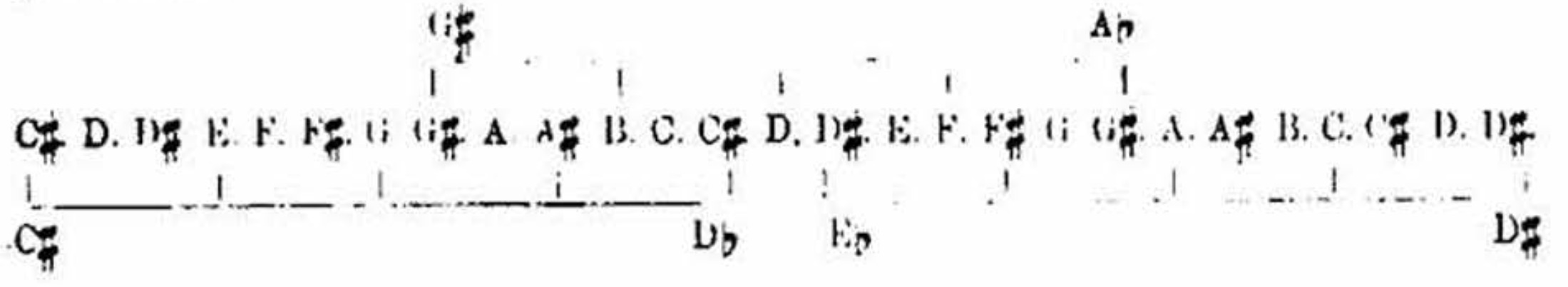
In the above line it will be readily observed that these three chromatic chords, having each of their intervals a minor third, involve, as necessary elements of their build, every one of the twelve semitones at one point or another of the line. This is a second witness to the legitimacy of the chromatic scale of twelve semitones. We have our first witness to the same in the evolution of the semitones progressively in the course of the modulations by which, in growth-like continuity, Nature links the successive keys; whether developed upward, as is the natural way of the majors; or downward, as in the natural way of the minors; or half upward and half downward, which is an expedient in order to simplify the signatures. In whichever direction the modulation is effected, one note is always divided, and must, true to Nature, be signified by placing a sharp or a ?, as the case may be, to the 4-comma altered interval, and this always leaves a 5-comma interval to occupy the place to which Nature has assigned such interval in the original scale. When this operation has been twelve times performed, we have the chromatic scale of twelve semitones. Thus by two witnesses the thing is established. By further examination of these chromatic chords we find other interesting features beside their witness to the twelve semitones of the octave. [Scientific Basis and Build of Music, page 56]
If we view the Diatonic scale from the standpoint of their harmonizing, it is the first five notes of the octave which are the natural scale. The eight notes of the octave form a compound scale. So, in this view, in the octave of notes we have before us two scales; and this is true in both major and minor modes after their own dual fashion. In each of these two diatonic modes, the major and the minor, there are two semitones; but there are only two semitones altogether in the twofold system. When the major is generated by itself it has them both; and when the minor is generated by itself it also has both; but when the major and the minor are generated simultaneously, or as one great dual outgrowth, while the major in the ascending Genesis is producing the semitone E-F, the third and fourth of its octave scale, the minor responsively in the descending Genesis is producing the semitone B-C, the second and third of its octave scale. In this view of them, therefore, the semitone E-F belongs genetically to the major, and B-C to the minor; and this claim is asserted in the major tonic chord C E G, in which its own semitone is [Scientific Basis and Build of Music, page 64]
embedded; and in the minor tonic chord A C E in the same way is embedded its own semitone; and in these chords they appear in their proper places as third and fourth, C, d, E f, G; and second and third, A, b C, d, E. It is these first five notes of the octave scale which in a very distinctive way constitute the natural scale, which can be harmonized consecutively in one manner. The octave is seen in this view to be a compound scale, inasmuch as a compounding method of harmonizing has to be resorted to in passing consecutively from the sixth to the seventh. Similar compounding has to be done in the minor as well.1 [Scientific Basis and Build of Music, page 65]
The peculiar effects are exhibited when the chord-scale is next set forth. We have seen that there are six chords evolved in the Genesis upward and downward, 3 in the major form and 3 in the minor. In the fifths of the minor the semitone is always in the lower third, occurring between the second and third in the subdominant and tonic, and between the first and second in the dominant chord; whereas in the major it is always in the upper third, between the fourth and fifth in the subdominant, and between the third and fourth in the tonic and dominant chords. While the thirds which the fifths contain are thus so varied, the fifths themselves have always one magnitude, whether major or minor. [Scientific Basis and Build of Music, page 68]
The Chromatic Scale is naturally the last to come into view, for it is not generated by a mathematical process at all. Chromatic intervals are indeed found in the scale as mathematically generated. The semitones between B-C and E-F are two chromatic intervals, and the chord which occurs between the major and the minor in the chord-scale when it begins with the minor mode is a chromatic chord, though in an uncompleted condition. But the making of the octave into a chromatic scale of twelve small or semi-tones, is the work of modulation from one key to another through the whole twelve keys in either the major or minor sphere; and this process is fully set forth in the pre-note to the chromatic treatise. [Scientific Basis and Build of Music, page 69]
- and it is balanced between the two forces. If the effects of notes or chords depended solely on their ratios, then the effect of the subdominant, tonic, and dominant would have been alike, for these chords have exactly the same ratios. The centrifugal force of the notes of the dominant chord would take if away from the tonic chord; but Nature, in her skill to build and mix, has in the octave scale placed the middle of the dominant B under the root of the tonic C, and the top of the dominant D under the middle of the tonic E; so that these two rising notes are inevitably resolved into the tonic chord. The gravitating tendencies of the notes of the subdominant would take it also away from the tonic; but in the octave scale Nature has placed the middle of the subdominant A above the top of the tonic G, and the root of the subdominant F above the middle of the tonic E; so that these two falling notes also are inevitably resolved into the tonic chord. In this way two notes resolve to the center of the tonic, D upwards and F downwards; one to the top, A to G, and one to the root, B to C. Nature has thus placed the notes which have upward tendencies under the notes having downward tendencies; she has also related them by proximity, the distance from the one to the other being always either a semitone or the small tone of the ratio 9:10. [Scientific Basis and Build of Music, page 95]
"Dividing the octave into twelve semitones is a near approach to the mathematical quantities, and this saves the musical artist from errors in tone - at least to any extent; but it does not save from errors in judgment. In the case of G#, for example, not one of the reasons given for the use of the sharp seventh in the minor scale is a correct one. A touch of nature makes the world akin, and a touch of the Law of Duality balances everything in music." [Scientific Basis and Build of Music, page 99]
When Leonhard Euler, the distinguished mathematician of the eighteenth century, wrote his essay on a New Theory of Music, Fuss remarks - "It has no great success, as it contained too much geometry for musicians, and too much music for geometers." There was a reason which Fuss was not seemingly able to observe, namely, that while it had hold of some very precious musical truth it also put forth some error, and error is always a hindrance to true progress. Euler did good service, however. In his letters to a German Princess on his theory of music he showed the true use of the mathematical primes 2, 3, and 5, but debarred the use of 7, saying, "Were we to introduce the number 7, the tones of an octave would be increased." It was wise in the great mathematician to hold his hand from adding other notes. It is always dangerous to offer strange fire on the altar. He very clearly set forth that while 2 has an unlimited use in producing Octaves, 3 must be limited to its use 3 times in producing Fifths. This was right, for in producing a fourth Fifth it is not a Fifth for the scale. But Euler erred in attempting to generate the semitonic scale of 12 notes by the use of the power of 5 a second time on the original materials. It produces F# right enough; for D27 by 5 gives 135, which is the number for F#. D27 is the note by which F# is produced, because D is right for this process in its unaltered condition. But when Euler proceeds further to use the prime 5 on the middles, A, E, and B, and F#, in their original and unaltered state, he quite errs, and produces all the sharpened notes too low. C# for the key of D is not got by applying 5 to A40, as it is in its birthplace; A40 has already been altered for the key of G by a comma, and is A40 1/2 before it is used for producing its third; it is A40 1/2 that, multiplied by 5, gives C#202 1/2, not C200, as Euler makes C#. Things are in the same condition with E before G# is wanted for the key of A. G# is found by 5 applied to E; not E in its original and unaltered state, E30; but as already raised a comma for the key of D, E30 3/8; so G# is not 300, as Euler has it, but 303 3/4. Euler next, by the same erroneous methods, proceeds to generate D# from B45, its birthplace number; but before D# is wanted for the key of E, B has been raised a comma, and is no longer B45, but B45 9/16, and this multiplied by 5 gives D#227 13/16, not D225, as Euler gives it. The last semitone which he generates to complete his 12 semitones is B?; that is A#, properly speaking, for this series, and he generates it from F#135; but this already altered note, before A# is wanted for the key of B, has been again raised a comma [Scientific Basis and Build of Music, page 107]
One purpose of this plate is to show that twelve times the interval of a fifth divides the octave into twelve semitones; and each of these twelve notes is the first note of a major and a minor scale. When the same note has two names, the one has sharps and the other has flats. The number of sharps and flats taken together is always twelve. In this plate will also be observed an exhibition of the omnipresence of the chromatic chords among the twice twelve scales. The staff in the center of the plate is also used as to show the whole 24 scales. Going from the major end, the winding line, advancing by fifths, goes through all the twelve keys notes; but in order to keep all within the staff, a double expedient is resorted to. Instead of starting from C0, the line starts from the subdominant F0, that is, one key lower, and then following the line we have C1, G2, etc., B6 proceeds to G? instead of F#, but the signature-number continues still to indicate as if the keys went on in sharps up to F12, where the winding line ends. Going from the minor end, the line starts from E0 instead of A0 - that is, it starts from the dominant of A0, or one key in advance. Then following the line we have B1, F#2, etc. When we come to D#5, we proceed to B? instead of A#6, but the signature-number continues as if still in sharps up [Scientific Basis and Build of Music, page 114]
In the festoons of ellipses the signatures are given in the usual conventional way, the major F having one flat and minor E having one sharp. The major and minor keys start from these respective points, and each successive semitone is made a new keynote of a major and a minor respectively; and each ellipse in the festoons having the key shown in its two forms; for example, in the major F, one flat, or E#, eleven sharps; in the minor E, one sharp, or F?, eleven flats. Thus is seen all the various ways that notes may be named. The four minor thirds which divide the octave may be followed from an ellipse by the curved lines on which the ellipses are hung; and these four always constitute a chromatic chord. [Scientific Basis and Build of Music, page 115]
The scales in this plate advance by semitones, not in their normal way by fifths; but their normal progress by fifths is shown by the spiral-ellipse line winding round under the stave and touching the ellipses containing the scales by semitonic advance; the scales being read to the right for the majors inside, and to the right for the minors outside. In each of the modes the scales are written in ?s and #s, as is usual in signatures; and since the scales [Scientific Basis and Build of Music, page 116]
advance by semitones, the keys with ?s and #s alternate in both modes. The open between G# and A? in the major, and between D# and E? in the minor, is closed in each mode, and the scale made one. The dotted lines across the plate lead from major to relative minor; and the solid spiral line starting from C, and winding left and right, touches the consecutive keys as they advance normally, because genetically, by fifths. The relative major and minor are in one ellipse at C and A; and in the ellipse right opposite this the relative to F# is D#, and that of G? and E?, all in the same ellipse, and by one set of notes, but read, of course, both ways. [Scientific Basis and Build of Music, page 117]
Hughes
The 18 tones of keyed instruments are represented round this circle, and again below in musical clef. As all, with the exception of G? and A#, become in turn either Major or Minor Key-notes, or both, no distinction is made between tones and semitones throughout the scheme. In this diagram the 12 Major Key-notes are written thus
"Harmony must be looked at in two ways at least: first, up the score from bottom to top—the perpendicular view; second, along the score from side to side—the horizontal view. Then as to its periods or pulsations—its to and fro, its flow and ebb. This brings us to rhythm and measure. At the bottom of these lie what is called stress or accent—emission and remission—strong and weak: of these the bar in modern music is an outward and visible sign of certain facts which ought to be in the music, but which, if not in the music, the presence of the bar is of no avail. The bar cannot give stress or accent. 'Wherever there is time, there must be accent;'* but the tick of a clock has no accent. Hullah (or Chorley) should have said life." "The semitone makes music. What operation has it upon the accent or to and fro? It creates the call, it supplies the answer." [This point, I believe, Dr. Gauntlett never alluded to with me, and I have feared that making no difference between tones and semitones might be considered a difficulty with regard to the scheme. In the working of the natural laws of harmony, they must all equally be employed.—F. J. H.] "Art (grand and true) does not depend upon the teaching of facts. The head is of less importance than the heart. Unless the tone of feeling, the habit and disposition, be well fixed, nothing enduring can come out of the misdirected artist." [Harmonies of Tones and Colours, Fragments from the Last Note-book, page 50]
See Also
apotome higher
apotome lower
apotome minor
Apotome Minor
apotome scales
Apotome
apotomes and skismas
Chromatic
comma
Diesis
equal temperament
Interval
Music
Note
pythagorean komma
Scale
semitonic
semitonic interval
skisma
Step
