

Mathematics is the study of quantity, structure, space, and change. Mathematicians seek out patterns, formulate new conjectures, and establish truth by rigorous deduction from appropriately chosen axioms and definitions.
Through the use of abstraction and logical reasoning, mathematics evolved from counting, calculation, measurement, and the systematic study of the shapes and motions of physical objects. Practical mathematics has been a human activity for as far back as written records exist. Rigorous arguments first appeared in Greek mathematics, most notably in Euclid's Elements. Mathematics continued to develop, for example in China in 300 BC, in India in AD 100, and in the Muslim world in AD 800, until the Renaissance, when mathematical innovations interacting with new scientific discoveries led to a rapid increase in the rate of mathematical discovery that continues to the present day. wikipedia
Keely
Keely writes: "The mathematics of vibratory etheric science, both pure and applied, require long and arduous research. It seems to me that no man's life is sufficient, with the most intense applications, to cover more than the introductory branch. The theory of elliptic functions, the calculus of probabilities, are but as pygmies in comparison to a science which requires the utmost tension of the human mind to grasp." [Snell Manuscript - The Book, page 2], [The Fountain Head of Force]
Russell
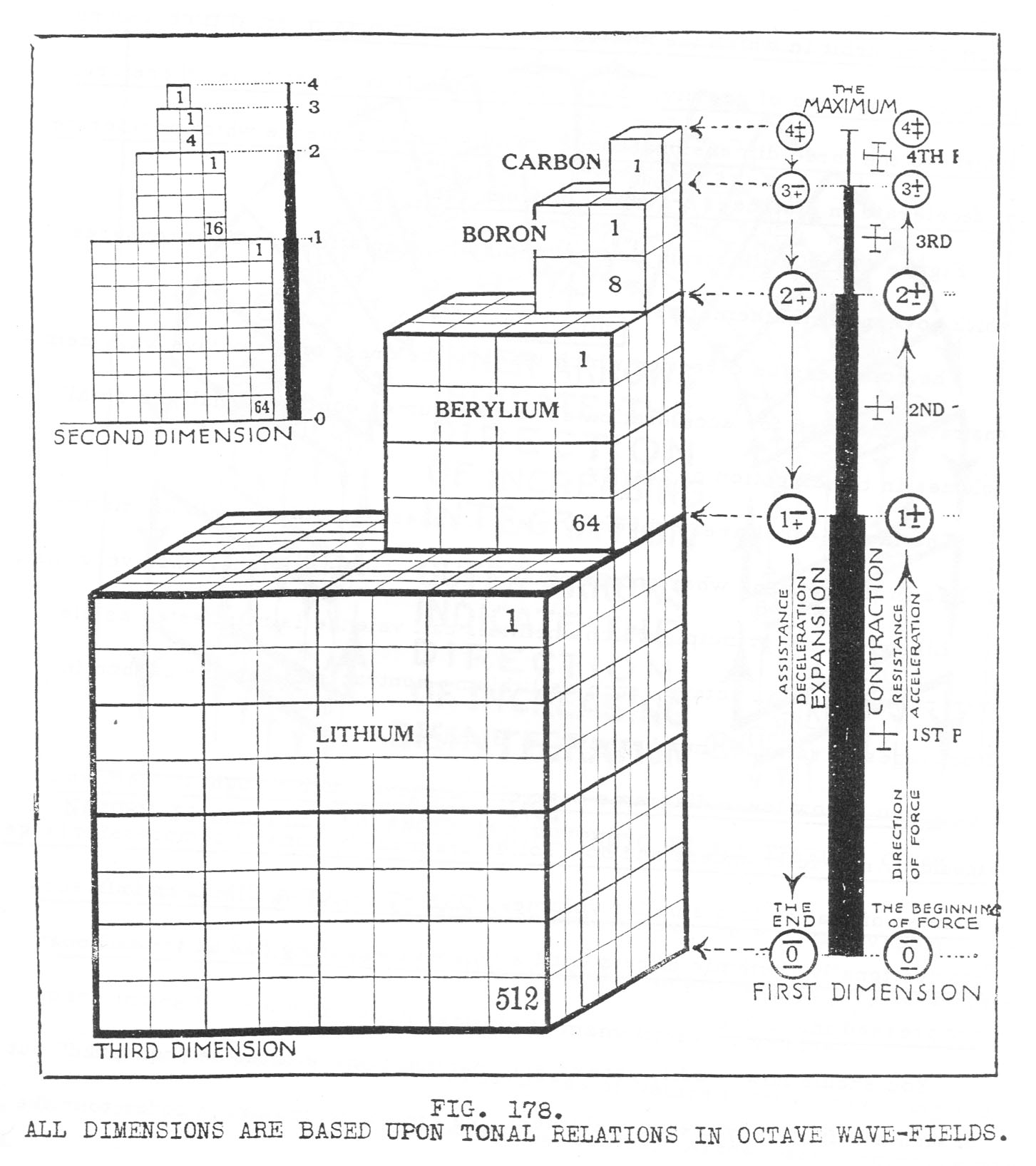
"Spheres occur only at wave amplitudes and the fact of its four positive and four negative efforts is the basis of the octave wave from which our spectrum, our octaves of the elements and our octaves of musical tones are derived.
"This 0, 1, 2, 3, 4, 4, 3, 2, 1, 0 octave sequence constitutes the heartbeat of the universe. It is the basis of our musical rhythms, our chemistry, our mathematics, our symmetry of design of all animal, mineral and vegetable forms and of our color spectrum of light." [Walter Russell, Home Study Course, 53 - Unit Nine - Lesson 35]
"The principle upon which universal mathematics is founded is the measure of plus and minus relationships between the various potential pressures of radial extensions from zero and back to zero. Whenever these mathematical relations balance with each other they are equi-potential and belong to the changeless spherical system of curvature in which all relations are in balance.
Whenever these relations are out of balance they are unequal in their potentials and belong to the ever changing radial system of curvature upon which there is constant change and consequent unbalance.
In the radial system of this three dimensional universe are two directions for computation of mathematical relations—1—the compressive direction of gravity which is accelerative as of its wave-field cube in inverse ratio—and 2—the expansive direction of radiation, which is decelerative as of the cube in direct ratio.
All other computations are based upon cross sections of this three dimensional cube-sphere universe. Planes cross sectioning a cube are two dimensional, hence the two dimensional computation is based upon the square and the one dimensional of length, breadth, or thickness is based upon the pressure and time relation of one point to another as of a straight line joining these two points.
There are no straight lines in Nature, however, for all direction in Nature is curved, and all curvature is spiral. All motion in one direction, is therefore, a part of an orbit in which the motion covers equal areas in equal time around its controlling zero of gravity. Every one dimensional relation is, therefore, subject to the three dimensional forces of this radial universe which accelerate or decelerate in distances traveled between radii.
Figure 178 will illustrate this principle of the relation of wave pressures which govern all mathematics.
The compression direction which leads to the crest of the octave wave demonstrates the need for acceleration as large volumes contract tonally to small volumes in the direction of gravity.
The law of equal areas covered in equal times is manifested in all matter as it is in the heavens where outer planets move slowly and inner ones move very fast.
Likewise, the principle which chemists call valence is manifested as element number 1 in an octave, such as lithium—contracts to become carbon in four stages of valence, numbered 1, 2, 3 and 4.
If you follow these diagrams carefully and give much thought to them you should by now fully understand how solids are made by tonally compressing large volumes of matter into smaller volumes, ONE STEP AT A TIME, in four successive tonally rhythmic efforts until a volume measuring 512 units has been compressed into 1 unit.
(courtesy University of Science and Philosophy)
(click to enlarge)
All dimensions are based upon tonal relations in octave wave-fields." [Walter Russell, Home Study Course, 67 - Unit Eleven - Lesson 43.2]
Nikola Tesla
“Today’s scientists have substituted mathematics for experiments, and they wander off through equation after equation, and eventually build a structure which has no relation to reality. ” [Nikola Tesla]
Rudolf Steiner
"Plato required those applying to his school to take a course in mathematics first. Since the strict laws of mathematics are not subject to the ordinary course of sensory phenomena, they make a very good preparation for seekers of knowledge, who must put aside personal arbitrariness and distractions if they wish to make progress in mathematics. Voluntarily overcoming all uncontrolled and arbitrary thinking prepares them for the task ahead. They learn to respond to only the requirements of thinking itself, since that is how they must proceed in all thought activity that serves spiritual knowledge. Their thinking must replicate the undisturbed results and conclusions of mathematics. Wherever they go, wherever they may be, they must always attempt to think in this way. Then the laws of the spiritual world, laws that pass through without a trace when thinking is of the everyday confused variety, can flow into them. Well-ordered thinking leads them from secure starting points to the most hidden truths. (These suggestions should not be taken one-sidedly, however - although mathematics is good practice and discipline for our thinking, it is certainly possible to learn pure, healthy and vital thinking without it.)" [Rudolf Steiner, Theosophy, 10th edition 1922, translated 1994, Anthroposophic Press, pp. 187-188]
Vedic Mathematics a surprisingly simple math system.
Nature's own art, not man's device, enables us to realize and represent all the harmonic progressions that belong to music. It has been nature's self to the practical and inspired musician. By the division of the octave into twelve semitones, he is emancipated from the restrictions and jargon which arise from misapplied mathematics. The mathematicians say that such and such things are wrong; the great masters in music inspirationally do these very things. [Scientific Basis and Build of Music, page 33]
Music, and mathematics have nothing more to do with it. Already the Law of Position has guided the Genesis upward in the major; and while mathematical primes were generating the chords one after another in precisely the same way and form, like peas in a pod, the Law of Position was arranging them one over the other, and so appointing them in their relative position each its own peculiar musical effect bright and brighter. And when the major had been thus evolved and arranged by ratios and position, another law, the Law of Duality, gave the mathematical operation its downward direction in the minor; and while the primes which measured the upward fifths of the major also measure the downward fifths of the minor, the Law of Position is placing them in their relative position, and appointing each its own peculiar effect grave and graver. [Scientific Basis and Build of Music, page 68]
Cayce
"Let yourself be in agreement with spiritual meaning or prompting; like the beauty of music, the rhythm in mathematics, the rhythm in the score in music and that which answers to the high emotions of affection, companionship, activities in your relationships." [Cayce (4028-1]
I have a question. Don't laugh. Mathematics is a collection of symbols which are to be interpreted within context (or something like that). The alphabet is a collection of symbols which when arranged in certain ways form words (which are also symbols) and words again arranged in certain ways become or describe ideas, concepts, etc. The question is: Why use math symbols (years to learn) when alphabet symbols (we already know) can do the job? Or am I missing something?
See Also
Addition
Algebraic Values of Trigonometric Functions
Arithmetic
Chord
Delta
Division
Geometry
Indig Numbers
Interval
law of multiple proportions
law of constant composition
Law of Definite Proportions
Maria Gaetana Agnesi
Multiplication
Music
Number
Proportion
Propositions of Geometry
Quantum Arithmetic
Ratio
Stoichiometry
Subtraction
Sympsionics
12.21 - Fibonacci Whole Numbers v Irrational Decimal near Equivalents
