Descending accent in musical notes. ?
Russell
"...when science discards its concept of matter as being substance, and becomes aware of the gyroscopic control of motion they will be able to split the carbon tone into isotopes as a musical tone is split into sharps and flats." [Walter Russell]
Ramsay
"Again, had the scales been properly derived from each other, the sharp of the one would always have been higher than the flat of the other;2 and instead of the flat being two commas, less the apotome minor, higher than the sharp, the sharp would have been the apotome minor, the ratio of 8192:8201 1/4, higher than the flat; and there would never have been more than the apotome minor between the sharp of the one and the flat of the other, except where the scales were nine and the notes themselves were twelve fifths apart, and then the difference would have been a comma and the apotome minor." [Scientific Basis and Build of Music, page 14]
The specific levity of notes increases in proportion to the number of times the ratios are multiplied in order to produce them, going upward by sharps; and their specific gravity increase in proportion to the number of times the ratios are divided in order to produce them, going downward by flats. The knowledge of this is attained when everything is in its perfect order. It is the discovery of the Law of Duality in music which shows the method of applying the ascending and the descending ratios so as to exhibit that perfect order of Nature. [Scientific Basis and Build of Music, page 43]
Through the whole system, in the progression of major scales with sharps and minor scales with flats, the new sharp is applied to the middle of the major dominants, and the new flat to the middle of the minor subdominants. In the progression of major scales with flats and minor scales with sharps, the new flat is applied to the root of the major subdominant, and the new sharp to the top of the minor dominant.2 [Scientific Basis and Build of Music, page 43]
It is according to the Law of Duality that the keys on the piano have the same order above and below D, and above and below G# and A?, which is one note. In these two places the dual notes are given by the same key; but in every other case in which the notes are dual, the order above the one and below the other is the same. The black keys conform to the scale, and the fingering conforms to the black keys. On that account in the major scale with flats, for the right hand the thumb is always on F and C; and as the duals of F and C are B and E in the minor scale with sharps, for the left hand thumb is always on B and E. [Scientific Basis and Build of Music, page 44]
The triplet B, D, F, has been called the imperfect triad, because in it the two diatonic semitones, B-C and E-F, and the two minor thirds which they constitute, come together in this so-called imperfect fifth. But instead of deserving any name indicating imperfection, this most interesting triad is the Diatonic germ of the chromatic chord, and of the chromatic system of chords. Place this triad to precede the tonic chord of the key of C major, and there are two semitonic progressions. Place it to precede the tonic chord of the key of F# major, and there are three semitonic progressions. Again, if we place it to precede the tonic chord of the key of A minor, there are two semitonic progressions; but make it precede the tonic chord of E? minor, and there are three semitonic progressions. This shows that the chromatic chord has its germ in, and its outgrowth from the so-called "natural notes," that is notes without flats or sharps, notes with white keys; and that these natural notes furnish, with only the addition of either A? from the major scale or G# from the minor, a full chromatic chord for one major and one minor chord, and a secondary chromatic chord for one more in each mode. [Scientific Basis and Build of Music, page 52]
But, as the subdominant sixth and dominant seventh suggest that the chromatic chord should be a 4-note chord, we must find out how Nature completes this diatonic chromatic triad and makes it a 4-note chord, and that according to its own intrinsic character as of minor thirds. Nature has always a rationale in her operations which it is ever delightful to discover. Wedged in between the minor dominant and the major subdominant, this triad, B D F, has already B, the top of the dominant minor, for its root; and F, the root of the subdominant major, for its top; and its middle is the mysterious D which, in its two positions as root of the minor subdominant and top of the major dominant, stands at the two extremes of the whole twofold diatonic key, bounding and embracing all; and which in its two degrees as D26 2/3 and D27 claims kindred with both minor and major modes of the twofold key system. Surely this Janus-faced D, looking this way toward the minor and that way to the major, seems to say, "the complement of this chord, of which I am the heart, is not far to seek nor hard to find on either side." It has already B in common with the minor dominant; the very next step is to the middle of this chord, G. Roots and tops of chords may not be altered, but middles may with impunity be flattened or sharpened as occasion may require. No two of them in succession in the chord-scale have the same structure; the chromatic triad, in claiming this middle, claims it sharpened, for it must have [Scientific Basis and Build of Music, page 54]
a minor third. So by adding the middle of the minor dominant, G, but made G#, that the third so produced may be a minor third, according to the nature of the chromatic chords, we have on this minor side of the chord G#, B, D, F, which we may call its minor form, inasmuch as the semitone of its second minor third is the one, B-C, which genetically arises in the minor genesis; and inasmuch as it has also received its supplemental G# from the minor dominant. How shall we find its complement on the other side? We have seen that D, the Janus-faced center of this triad, B, D, F, looks, as D27, toward the major also; it has already F in common with the major subdominant. The very next step is to the middle of this chord, A. Middles, we have just seen, are ever ready to accommodate themselves; and this minor third triad claims that A be flat|flattened, for on this side also, though its major side, it must have a minor third; so by adding the middle of the major subdominant, A, but made A?, according to the nature of chromatic intervals, that this F-A? also may be a minor third; and now we have it as B, D, F, A?, which we may call its major form, inasmuch as the semitone of its minor third, E-F, is the one which genetically arises in the major genesis, and inasmuch as it has now received its supplemental A? from the major subdominant. This, then, is the chromatic chord in its native place, and in its native constitution; a 4-note chord, wholly of the minor thirds. It will be observed that it has now, in its two forms, divided the octave into minor thirds - 4 minor thirds, so it is very much at home anywhere in the octave; indeed it is at home everywhere - G#, B, D, F, A?. And as every diatonic common chord in music is constituted of materials found in the octave of notes, it cannot be far from a chromatic chord in some one of its forms. [Scientific Basis and Build of Music, page 55]
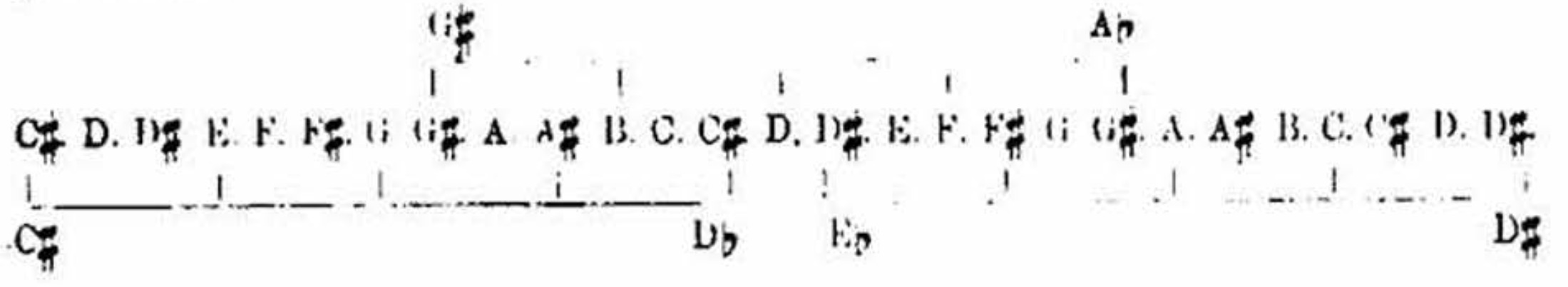
In the above line it will be readily observed that these three chromatic chords, having each of their intervals a minor third, involve, as necessary elements of their build, every one of the twelve semitones at one point or another of the line. This is a second witness to the legitimacy of the chromatic scale of twelve semitones. We have our first witness to the same in the evolution of the semitones progressively in the course of the modulations by which, in growth-like continuity, Nature links the successive keys; whether developed upward, as is the natural way of the majors; or downward, as in the natural way of the minors; or half upward and half downward, which is an expedient in order to simplify the signatures. In whichever direction the modulation is effected, one note is always divided, and must, true to Nature, be signified by placing a sharp or a ?, as the case may be, to the 4-comma altered interval, and this always leaves a 5-comma interval to occupy the place to which Nature has assigned such interval in the original scale. When this operation has been twelve times performed, we have the chromatic scale of twelve semitones. Thus by two witnesses the thing is established. By further examination of these chromatic chords we find other interesting features beside their witness to the twelve semitones of the octave. [Scientific Basis and Build of Music, page 56]
In the same way, but inversely, and still under the Law of Duality, the middle of the subdominant minor is lowered a flat. F#67 1/2 in the key of E minor is F64 in the key of A; B45 in the key of A is B?42 2/3 in the key of D; E60 in the key of D is E?56 8/9 in the key of G. This lowering by flats of the subdominant middle in the minors, responsive to the raising by sharps of the dominant middle in the majors, goes on through all the twelve minor keys.1 [Scientific Basis and Build of Music, page 62]
lastly it is altered again and becomes, by the power of 3 once more, F#,#, and serves in four keys. But this carries us beyond the horizon of our musical world of twelve keys; for in B#, the top of the tonic E, we have reached our twelfth fifth, and it here coalesces with C of the seventh octave, and closes the circle. This is the way that all notes become alternately altered, either by commas and sharps in the upward genesis of scales, or by commas and flats in the downward Genesis, by the alternate powers of 3 and 5. In the upward Genesis in this illustration, notes by the power of 5 serve in three keys, and those by the power of 3 serve in four keys. In the minors it is just the inverse on this by the Law of Duality. But no note serves for more than either three or four keys, as the case may be. [Scientific Basis and Build of Music, page 63]
G# as it occurs in the scales of A, E, and B major, and A? as it occurs in the scales of F and B? minor, are only distant the apotome minor, and are well represented by one key of the piano. It is only G# as it occurs in the scale of F six sharps major, and A? as it occurs in the scale of E six flats minor, that is not represented on the piano. These two extreme notes F# and E? minor are at the distance of fifteenth fifths and a minor third from each other. This supplies notes for 13 major and 13 minor mathematical scales; but as this is not required for our musical world of twelve scales, so these far-distant G# and A? are not required. The piano is only responsible for the amount of tempering which twelve fifths require, and that is never more than one comma and the apotome minor. [Scientific Basis and Build of Music, page 80]
N.B. - The flat comes here by the prime 5, and the comma by the prime 3. Now we have the key of D provided for:-
The six successive major scales with sharps require two new notes each; and so with the six successive scales with flats, they also require two new [Scientific Basis and Build of Music, page 88]
In a similar and responsive way Duality provides for the six major scales with flats.
The two new notes required for the scale of
F major are the B? of D, and the D of A minor;
for B? major, the E? of G, and the G of D minor;
for E? major, the A? of C, and the C of G minor;
for A? major, the D? of F, and the F of C minor;
for D? major, the G? of B?, and the B? of F minor;
for G? major, the C? of E?, and the E? of B? minor.1 [Scientific Basis and Build of Music, page 90]
The scales march on following each other methodically, whether they be written with sharps or flats, and
"Not a step is out of tune, as the tides obey the moon."
The most natural, because the genetic, way to write the scales is to make the major scales all in sharps, after C, because the major genesis is upward in ratios ascending; and to make the minor scales all in flats, after A, because the minor genesis is downward in ratios descending. Let the young student, however, always keep in mind that the sharps and flats are simply marks to show how Nature, at whatever pitch we are taking the scales, is securely keeping them in the same form as when they are first generated; and in their birthplace no sharps or flats are needed. [Scientific Basis and Build of Music, page 90]
sexual note in the scales of G major and E minor are the two A's; in D major and B minor, the two E's; in A major and F# minor, the two B's; in E major and C# minor, the two F's; in B major and G# minor, the two C's; and in F# major and D# minor, the two G's. These two last scales being the beginning of a second cycle of twelve scales when the scales are written half in flats and half in sharps, as we have done them in this case. Turning to the other half of our circle, those which we have, and which usually in music books are, written in flats, in F major and D minor the sexual notes are the two G's; in B? and G, the two C's, in E? and C, the two F's; in A? and F, the two B's; in D? and B?, the two E's; and in G? and E?, the two A's. [Scientific Basis and Build of Music, page 91]
In the opening of the third measure the tune returns to its own key by striking the tonic. This case is a very simple illustration of how a composition will move with perfect naturalness in more keys than one, the keys so grow out of each other, and may either merely snatch a passing chord from a new key, or pass quite into it for a phrase or two, or for a whole measure, then return as naturally, either by a smooth and quiet or by a strongly contrasted turn, according to the chords between which the turn takes place. In such modulation there may or there may not be marked a sharp, ?, or ?, in the air itself; the note which Nature raises in the new key may occur in one of the other parts of the harmony. In Watchman it is A, the fourth, which is altered; from being ? it is made ?. The change which takes place in the sixth of the scale, which is C in Watchman, is only one comma, the ratio of 80 to 81, and it slips into the new key as if nothing had happened. No mark is placed to it, as the comma difference is never taken notice of, although it is really and regularly taking place, with all the precision of Nature, in every new key. It is, however, only the note which is altered four commas, which is marked by a sharp, ?, or ?, as the case may be. [Scientific Basis and Build of Music, page 94]
The Plate shows the Twelve Major and Minor Scales, with the three chords of their harmony - subdominant, tonic, and dominant; the tonic chord being always the center one. The straight lines of the three squares inside the stave embrace the chords of the major scales, which are read toward the right; e.g., F, C, G - these are the roots of the three chords F A C, C E G, G B D. The tonic chord of the scale of C becomes the subdominant chord of the scale of G, etc., all round. The curved lines of the ellipse embrace the three chords of the successive scales; e.g., D, A, E - these are the roots of the three chords D F A, A C E, E G B. The tonic chord of the scale of A becomes the subdominant of the scale of E, etc., all round. The sixth scale of the Majors may be written B with 5 sharps, and then is followed by F with 6 sharps, and this by C with 7 sharps, and so on all in sharps; and in this case the twelfth key would be E with 11 sharps; but, to simplify the signature, at B we can change the writing into C, this would be followed by G with 6 flats, and then the signature dropping one flat at every new key becomes a simpler expression; and at the twelfth key, instead of E with 11 sharps we have F with only one flat. Similarly, the Minors make a change from sharps to flats; and at the twelfth key, instead of C with 11 sharps we have D with one flat. The young student, for whose help these pictorial illustrations are chiefly prepared, must observe, however, that this is only a matter of musical orthography, and does not practically affect the music itself. When he comes to the study of the mathematical scales, he will be brought in sight of the exact very small difference between this B and C?, or this F# and G?; but meanwhile there is no difference for him. [Scientific Basis and Build of Music, page 108]
In the center column are the notes, named; with the lesser and larger steps of their mathematical evolution marked with commas, sharps, and flats; the comma and flat of the descending evolution placed to the left; the comma and sharp of the ascending evolution to the right; and in both cases as they arise. If a note is first altered by a comma, this mark is placed next to the letter; if first altered by a sharp or flat, these marks are placed next the letter. It will be observed that the sharpened note is always higher a little than the note above it when flattened; A# is higher than ?B; and B is higher than ?C, etc.; thus it is all through the scales; and probably it is also so with a fine voice guided by a true ear; for the natural tendency of sharpened notes is upward, and that of flattened notes downward; the degree of such difference is so small, however, that there has been difference of opinion as to whether the sharp and ? have a space between them, or whether they overlap, as we have shown they do. In tempered instruments with fixed keys the small disparity is ignored, and one key serves for both. In the double columns right and left of the notes are their mathematical numbers as they arise in the Genesis of the scales. In the seven columns right of the one number-column, and in the six on the left of the other, are the 12 major and their 12 relative minor scales, so arranged that the mathematical number of their notes is always standing in file with their notes. D in A minor is seen as 53 1/3, while the D of C major is 54; this is the comma of difference in the primitive Genesis, and establishes the sexual distinction of major and minor all through. The fourth of the minor is always a comma lower than the second of the major, though having the same name; this note in the development of the scales by flats drops in the minor a comma below the major, and in the development of the scales by sharps ascends in the major a comma above the minor. In the head of the plate the key-notes of the 12 majors, and under them those of their relative minors, are placed over the respective scales extended below. This plate will afford a good deal of teaching to a careful student; and none will readily fail to see beautiful indications of the deep-seated Duality of Major and Minor. [Scientific Basis and Build of Music, page 109]
When the major and minor scales are generated to be shown the one half in #s and the other half in ?s, it is not necessary to carry the mathematical process through the whole 24, as when the majors are all in #s and the minors all in ?s; because when six majors have been generated in #s, they furnish the new notes needed by the six relative minors; and when six minors have been generated in ?s, they furnish the new notes for the six relative majors. This plate begins with the major in C and the minor in A. The notes of these two are all identical except the D, which is the sexual note, in which each is not the other, the D of the minor being a comma lower than the D of the major. Going round by the keys in #s, we come first to E minor and G major. G major has been mathematically generated, and the relative minor E gets its F# from it; but the D of C major must also be [Scientific Basis and Build of Music, page 112]
Starting again at C major and A minor and going round by the keys in ?s, we come first to D minor and F major. The major gets its ? fourth from the ? sixth of the relative minor; and as the interval between D-E, the major sixth and seventh, must be a 9-comma interval, and its own D-E is only an 8-comma one, it must take the D of A minor, which is a comma lower, and this will correctly show the 9-comma interval between D and E. This is the way of their mutual providing in the region of ?s; the ? sixth of the minor is given to be the ? fourth of the relative major; and the comma-lower fourth of the sub-relative minor becomes the correct sixth of the major. The arrows indicate the source from which, and the place to which; the new notes come and go. [Scientific Basis and Build of Music, page 113]
The signature of major and relative minor is always the same whether in #s or ?s; but in the keys with #s in the plate the signature is only given on the major stave, to indicate that generating upwards is its natural way; and in the keys with ?s the signature is only placed in the minor stave, to indicate that generating downward is the natural way for the minor mode. [Scientific Basis and Build of Music, page 113]
When Plate XIII. is divided up the middle of the column, as in Plate XIV., so as that one side may be slipped up a fifth, representing a new key one-fifth higher, its subdominant made to face the old tonic, the two new notes are then pictorially shown, the second being altered one comma and the seventh four commas. The key at this new and higher pitch is by Nature's unfailing care kept precisely in the same form as the first; and wherever the major scale is pitched, higher or lower, the form remains unaltered, all the intervals arranging themselves in the same order. The ear, and the voice obedient to it, carry Nature's measuring-rule in them, and the writing must use such marks as may truly represent this; hence the use of sharps, flats, and naturals; these, however, be it observed, are only marks in the writing; all is natural at any pitch in the scale itself. All this is equally true of the minor mode at various pitches. These two plates are only another and more pictorial way of showing what the stave and the signature are usually made to express. [Scientific Basis and Build of Music, page 114]
One purpose of this plate is to show that twelve times the interval of a fifth divides the octave into twelve semitones; and each of these twelve notes is the first note of a major and a minor scale. When the same note has two names, the one has sharps and the other has flats. The number of sharps and flats taken together is always twelve. In this plate will also be observed an exhibition of the omnipresence of the chromatic chords among the twice twelve scales. The staff in the center of the plate is also used as to show the whole 24 scales. Going from the major end, the winding line, advancing by fifths, goes through all the twelve keys notes; but in order to keep all within the staff, a double expedient is resorted to. Instead of starting from C0, the line starts from the subdominant F0, that is, one key lower, and then following the line we have C1, G2, etc., B6 proceeds to G? instead of F#, but the signature-number continues still to indicate as if the keys went on in sharps up to F12, where the winding line ends. Going from the minor end, the line starts from E0 instead of A0 - that is, it starts from the dominant of A0, or one key in advance. Then following the line we have B1, F#2, etc. When we come to D#5, we proceed to B? instead of A#6, but the signature-number continues as if still in sharps up [Scientific Basis and Build of Music, page 114]
In the festoons of ellipses the signatures are given in the usual conventional way, the major F having one flat and minor E having one sharp. The major and minor keys start from these respective points, and each successive semitone is made a new keynote of a major and a minor respectively; and each ellipse in the festoons having the key shown in its two forms; for example, in the major F, one flat, or E#, eleven sharps; in the minor E, one sharp, or F?, eleven flats. Thus is seen all the various ways that notes may be named. The four minor thirds which divide the octave may be followed from an ellipse by the curved lines on which the ellipses are hung; and these four always constitute a chromatic chord. [Scientific Basis and Build of Music, page 115]
These two plates show the chromatic chord resolving into the twelve major and twelve minor tonic chords of the twenty-four scales. There seems to be twenty-five, but that arises from making G? and F# in the major two scales, whereas they are really only one; and the same in the minor series, E? and D# are really one scale. C in the major and A in the minor, which occur in the middle of the series, when both sharps and flats are employed in the signatures, are placed below and outside of the circular stave to give them prominence as the types of the scale; and the first chromatic chord is seen with them in its major and minor form, and its typical manner of resolving - the major form rising to the root, and falling to the top and middle; the minor form falling to the top, and rising to the root and middle. The signatures of the keys are given under the stave. [Scientific Basis and Build of Music, page 116]
The scales in this plate advance by semitones, not in their normal way by fifths; but their normal progress by fifths is shown by the spiral-ellipse line winding round under the stave and touching the ellipses containing the scales by semitonic advance; the scales being read to the right for the majors inside, and to the right for the minors outside. In each of the modes the scales are written in ?s and #s, as is usual in signatures; and since the scales [Scientific Basis and Build of Music, page 116]
advance by semitones, the keys with ?s and #s alternate in both modes. The open between G# and A? in the major, and between D# and E? in the minor, is closed in each mode, and the scale made one. The dotted lines across the plate lead from major to relative minor; and the solid spiral line starting from C, and winding left and right, touches the consecutive keys as they advance normally, because genetically, by fifths. The relative major and minor are in one ellipse at C and A; and in the ellipse right opposite this the relative to F# is D#, and that of G? and E?, all in the same ellipse, and by one set of notes, but read, of course, both ways. [Scientific Basis and Build of Music, page 117]
This diagram shows pictorially the open in the spiral of the mathematical scales, in which, if written in sharps only, B# is seen a little, that is, a comma and the apotome minor, in advance of C, and as the first scale of the new cycle; for it is a violation of Nature's beautiful steps to call it a thirteenth scale of this order, since every scale in the order is 31 commas in advance of the preceding, whereas B# is only one comma and a small fraction in advance of C. If the scales be written in ?s and #s for convenience of signature, then G# is seen a comma and apotome in advance of A?; while the whole circle of keys advancing by fifths are each 31 commas in advance of the preceding. We may therefore cast utterly from us the idea of there being more than twelve mathematical scales, and view the so-called thirteenth as simply the first of a new round of the endless spiral of scales. There is, however, in this note a banner with the strange device, "Excelsior," for it leads us onward into ever-advancing regions of vibrations, and would at last bring us to the ultimate and invisible dynamic structure of the visible world. The tempered system of 12 keys, as in Fig. 1, is by causing the G# and A? to coalesce and be one, as the two D's are already literally one by Nature's own doing. [Scientific Basis and Build of Music, page 118]
This plate, in the outer stave, has the 32 notes which arise with mathematical development of twelve scales in advancing fifths. The notes are marked with sharps, flats, and commas. The flats and commas of lowering are placed on the left of the notes, in the order in which they arise, reading them from the note downward; the sharps and commas of rising on the right, also reading from the note upward. The whole of these 32 notes are brought within the compass of an octave. [Scientific Basis and Build of Music, page 119]
In Fig. 1 is shown the way in which duality arranges the new sharp in the majors to the middle of the dominant, and the new flat to the middle of the subdominant in the minors, all through the six scales done in flats and sharps. The flat goes to the root of the subdominant and the sharp to the top of the dominant in the other six, as in Fig. 2. This is the invariable way that the new sharps and flats are responsively added all through the system. [Scientific Basis and Build of Music, page 120]
Hughes
I had for a long time studied the development of the harmonics of colour, and believed that I had gained them correctly; but I saw no way of proving this. The thought occurred—Why not test the laws in musical harmonies? I wrote down the development of the seven major keys of the white notes in keyed instruments. I was perplexed by the movement as of "to and fro," but the development of numbers explained this point, and I found that the method of development in colours, tones, and numbers agreed. I remembered the keys with sharps, but had forgotten that B? belonged to the key of F, and here I thought that the laws failed. But I found by reference that all were correct, the eighth being the first of a higher series, the laws having enabled me to distinguish between flats and sharps, [Harmonies of Tones and Colours, General Remarks on Harmonies of Tones and Colours, page 12]
whether veering round, or advancing and retreating in musical clef. I next tried the major keys which develope flats, and I thought that G? would develope a perfect harmony, but found that it must be F#, and that in this one harmony E# must be used in place of F?; on reference, I found that thus the twelve keys developed correctly in succession, the thirteenth being the octave, or first of a higher series. [Harmonies of Tones and Colours, Dr. Gauntletts Remarks1, page 13]
The twelve which develope twelve major harmonies are written thus
the other six which are incapabable of developing major harmonies thus
without regard to musical time. The seven colours are shown to answer to the seven white notes, the other five being intermediate tones and colours. A flat marked to a note indicates that it is nearer to the tone or colour below; a sharp means that it is nearer to the tone or colour above. The notes and chasms are not written according to accurately measured degrees. [Harmonies of Tones and Colours, Diagram I - The Eighteen Tones of Keyed Instruments, page 22a]
the 7 white notes of a keyed instrument are here coloured; the intermediate tones, shown by a flat or a sharp marked to a note, are left uncoloured, being intermediate tints. [Harmonies of Tones and Colours, Diagram I - Eighteen Tones of Keyed Instruments, page 22c]
We here trace the twelve harmonies developing in succession. Notice how exactly they all agree in their mode of development; also the use of the chasms between E and F, B and C. Remark also the beautiful results from the working of the double tones, especially C#-D?, and E#-F?, causing the seven tones of each harmony, when ascending, to rise one tone, and, descending, to reverse this movement. F#-G? is the only double tone which acts as F# when a key-tone, and G? when the root of D?. The root of each harmony is the sixth and highest tone in each succeeding harmony, rising one octave; when it is a double tone, it sounds according to the necessity of the harmony. The intermediate tones are here coloured, showing gradual modulation. The isolated fourths (sounding sevenths) were the previously developed key-tones; these also alter when they are double tones, according to the necessity of the harmony. Beginning with B, the isolated fourth in the harmony of C, the tones sound the twelve notes of a keyed instrument, E# being F?, and the double tones, some flats, some sharps. [Harmonies of Tones and Colours, Combinations of dissonance, rests, page 24]
The only exception is the double tone F#-G?, which is a curious study. F# as a harmony takes the double tones as sharps, and F? is E#. G? is also a harmony sounding the same tones, by taking the double tones as flats, and B? as C?. F# therefore takes the imperfect tone of E#, and G? the imperfect tone of C?. (See here the harmony of G? in musical clef.) [Harmonies of Tones and Colours, Combinations of dissonance, rests, page 24]
We find that on a keyed instrument each primary sounds the same tones as the secondaries of each third harmony below, but in a different order, and the double tones are altered sharp or flat as the harmony requires. For example, the secondaries of B are sharps; when primaries of D?, they are flats. In order to trace this quickly, the sharps and flats are written to each note. [Harmonies of Tones and Colours, Combinations of dissonance, rests, page 24]
The Major Key-note of C is here shewn developing its trinities from within itself, veering round; C and the other 11 developing their trinities in musical clef. Below each is the order in which the pairs meet, avoiding consecutive fifths. Lastly, C# is seen to be an imperfect major harmony; and G?, with B as C?, make the same harmony as F#. The intermediate tones of sharps and flats of the 7 white notes are here coloured in order to shew each harmony, but it must be remembered that they should, strictly, have intermediate tints. [Harmonies of Tones and Colours, The Major Keynote of C, page 24c]
This diagram represents the two last major primaries of a series of 12; 12 of a higher series follow, and the two first of a still higher series: the secondaries are written below the primaries, the sharps or flats belonging to the different harmonies are written to each note. Each primary sounds the same tones as the secondaries of each third harmony below, but in a different order; and the double tones are altered sharp or flat as the harmonies require.
By reference to previous coloured notes it will be seen that all these agree. [Harmonies of Tones and Colours, The Two Last Major Primaries, page 24e]
The twelve key-notes, with the six notes of each as they veer round in trinities, are again written in musical clef, and the scales added. The key-note leads the scale, and, after striking the two next highest notes of the seven of the harmony, goes forward, with its four lowest, an octave higher. The seven of each harmony have been traced as the three lowest, thus meeting the three highest in three pairs, the fourth note being isolated. Notwithstanding the curious reversal of the three and four of the scale, the three lowest pair with the three highest, and the fourth with its octave. The four pairs are written at the end of each line, and it will be seen how exactly they all agree in their mode of development. Keys with sharps and keys with flats are all mingled in twelve successive notes. If we strike the twelve scales ascending as they follow each other, each thirteenth note being octave of the first note of the twelve that have developed, and first of the rising series, the seventh time the scales gradually rise into the higher series of seven octaves beyond the power of the instrument. Descending is ascending reversed. After the seven and octave of a scale have been sounded ascending, the ear seems to lead to the descending; but ten notes of any scale may be struck without the necessity of modulation; at the seventh note we find that the eleventh note in the progression of harmonics rises to meet the seventh. For instance, B, the seventh note in the scale of C, must have F#. This point will be fully entered into when examining the meeting of fifths. To trace the scale of C veering round as an example for all, we may begin with C in Diagram II., and go forward with F, G, A, and B an octave higher. If the twelve scales were traced veering round, they would be found to correspond with the twelve as written in musical clef. [Harmonies of Tones and Colours, Diagram IV - The Development of the Twelve Major Scales, page 26a]
THE twelve keys have been traced following each other seven times through seven octaves, the keys mingled, the thirteenth note being the octave, and becoming first of each rising twelve. Thus developing, the seven notes of each eighth key were complementary pairs, with the seven notes of each eighth key below, and one series of the twelve keys may be traced, all meeting in succession, not mingled. When the notes not required for each of the twelve thus meeting are kept under, the eighths of the twelve all meet by fifths, and as before, in succession, each key increases by one sharp, the keys with flats following, each decreasing by one flat; after this, the octave of the first C would follow and begin a higher series. It is most interesting to trace the fourths, no longer isolated, but meeting each other, having risen through the progression of the keys to higher harmonies. In the seven of C, B is the isolated fourth, meeting F#, the isolated fourth in the key of G, and so on. Each ascending key-note becomes the root of the fifth key-note higher; thus C becomes the root of G, &c. [Harmonies of Tones and Colours, Diagram VII - The Modulating Gamut of the Twelve Keys1, page 29]
In the development of the key-notes, the sharp or flat is written to each note, but not to the keys. The reversal of the three and four notes of each seven of the twelve key-notes and their trinities meeting by fifths having been traced, we will now examine the twelve scales meeting by fifths, and the results arising from the reversal of the three and four notes of each fifth lower scale in the fifth higher. Take as an example the scale of C: C D E F G A B, and that of G: G A B C D E F#. The four lowest notes of the seven of C are the four highest, an octave higher, in G; F, the central and isolated note of the seven of C, having risen a tone higher than the octave in the scale of G. The twelve scales thus modulate into each other by fifths, which sound the same harmonies as the key-notes and their trinities. Refer to the twelve scales written in musical clef ascending by fifths, and strike them, beginning at the lowest C in the bass clef; this scale sounds no intermediate tones, but these must be struck as required for all the scales to run on in fifths. After striking the seven notes of C, if we fall back three, and repeat them with the next four notes of the seven; or strike the seven and octave of C, and fall back four, repeating them and striking the next four, the four last notes of each scale will be found to be always in the harmony of the four first of the fifth higher scale. When the twelve scales ascending have been thus gained, as we trace them also on the table, they may be struck descending by following them as written in musical clef upwards, and [Harmonies of Tones and Colours, Diagram VII - The Modulating Gamut of the Twelve Keys2, page 30]
THE term "key" in the minor developments must be taken in the sense in which it is understood by musicians, although it will be seen that it is only the seven of the harmony that are the relative minor keys of the majors, the scales with their chords sounding other keys. The grandeur, combined with simplicity, of the laws which develope musical harmonies are strikingly exhibited in the minor keys. Although at first they appear most paradoxical, and, comparing them with the majors, we may almost say contradictory in their laws of development, when they are in some degree understood, the intricacies disappear, and the twelve keys follow each other (with the thirteenth octave), all exactly agreeing in their mode of development. I shall endeavour to trace them as much as possible in the same manner as the majors, the lowest developments of the minor keys being notes with scales and chords, the notes always sounding their major harmonies in tones. Here an apparently paradoxical question arises. If the major keys are gained by the notes sounding the major tones, how are the minor keys obtained? Strictly speaking, there are no minor key-notes: the development of a minor harmony is but a mode of succession within the octave, caused by each minor key-note employing the sharps or flats of the fourth major key-note higher; and with this essential difference, it will be seen in how many points the developments of major and minor harmonics agree. I have carefully followed the same laws, and if any capable mind examines the results, I am prepared for severe criticism. I can only express that it was impossible to gain any other results than the seven of the harmony, the ascending and the descending scale and the chords combining three different keys. [Harmonies of Tones and Colours, Diagram VIII - On the Development of the Twelve Minor Harmonies, page 32]
When the twelve minor harmonies are traced developing in succession, we notice how exactly they all agree in their method of development, also the use of the chasms and the double tones, the seven of each harmony rising a tone when ascending, but reversing the movement in descending; keys with sharps and those with flats are mingled. The intermediate tones are here coloured, showing gradual modulation. D? is shown to be an imperfect minor harmony, and E?, by employing B as C?, is seen to be equivalent to D#. [Harmonies of Tones and Colours, Diagram IX - The Minor Keynote A and Its Six Notes, page 34a]
The diagram represents the Minor Key-note A and its 6 notes veering round in trinities; A and the other 11 developing their trinities in musical clef. Below each is the order in which the pairs unite, avoiding consecutive fifths, Lastly, D? is shewn to be an imperfect minor harmony, and by employing B as C?, E? is seen to be the same harmony as D#. As before, it should be remembered that the sharp and flat notes should, strictly, have intermediate tints. [Harmonies of Tones and Colours, The Diagram Represents the Minor Keynote, page 34c]
This diagram shews the two last minor primaries of a series of 12, with the 12 of a higher series, and the two first of a series higher still. As in the diagram of the Major, the secondaries are written below the primaries, and the sharps or flats of each harmony are written to their respective notes. With the exception that one of the primaries rises a tone higher, it will be observed that in the same way the notes of each minor primary are identical with the secondaries of each third harmony below, but in a different order; and the double tones are altered sharp or flat, as before. [Harmonies of Tones and Colours, Diagram Shews the Two Last Primaries, page 34e]
The seven of each harmony, with its scale. Sharps or flats, which vary in the scales from the harmonies, are written to each note, and only govern that one note. The scales are written as they pair. [Harmonies of Tones and Colours, The Seven of Each Harmony, page 35e]
The roots of the Minor Chord. The difference between a Major and a Minor Chord. The chords of the 12 keys follow. The sharps or flats that vary from the seven of the harmony, in the scales written to each note. The last descending chord is here seen to be the same as the first ascending, but this repetitive chord is only written in A. [Harmonies of Tones and Colours, The Roots of the Minor Chord, page 36c]
We may also examine the table of the twelve tones gained through seven octaves: the sharp or flat is written to each note, excepting in the keys as they unite in succession. Each key-note by fifths is seen to become a root of the fifth higher key-note: thus A becomes the root of E, and so on. In descending, each root of the fifth lower seven becomes the fifth higher key-note; the key-note D has G for its root, and so on. [Harmonies of Tones and Colours, Diagram XIV - The Modulating Gamut of the Twelve Minor Keys by Fifths1, page 39]
If we strike the ascending scales as written in musical clef again, beginning with the lowest A in the bass clef, we see that the second and sixth notes of each scale meet in higher harmony; the sharp or flat of the scale which varies from the seven notes of its harmony is written to each note. We descend as written in musical clef upwards; each third and seventh note meet in lower harmony, and thus all exactly agree in their mode of development. Having examined the scales as written in the table below, where the sharp or flat as before is marked to each note, but not to the keys, let us strike the key-notes, trinities, scales, and chords. The three harmonies of each key are written at the end of each line of musical clef. To descend, we follow the musical clef upwards, as before. [Harmonies of Tones and Colours, Diagram XIV - The Modulating Gamut of the Twelve Minor Keys by Fifths2, page 40]
TO recapitulate from the beginning, observe, firstly, the twelve major key-notes as they have developed from within themselves in succession, six tones in trinities seven times through seven octaves, each thirteenth note being the octave of the first note of the twelve that have developed, and being also the first of the higher series. We may retrace all as still sounding their tones, the key-notes leading the ear to the six notes of each harmony, the keys with sharps and those with flats being mingled. The ascending and descending scales always agree in their harmonies with the key-notes and their trinities. [Harmonies of Tones and Colours, Diagram XV - The Twelve Major and the Twelve Minor Keys, page 42a]
See Also
chromatic
Ramsay - PLATE XXVII - The Mathematical Scale of Thirty two notes in Commas, Sharps and Flats
semitone
