noun: a set of similar things that follow one after another
noun: a set of television or radio programs that are all about a particular subject, person, or group of people
noun: a set of books, documents, etc. that are published with the same design in order to show that they belong to the same group
noun: a set of related products, especially cars, made with the same basic design by a particular company
noun: a set of games played over a period of time between two teams
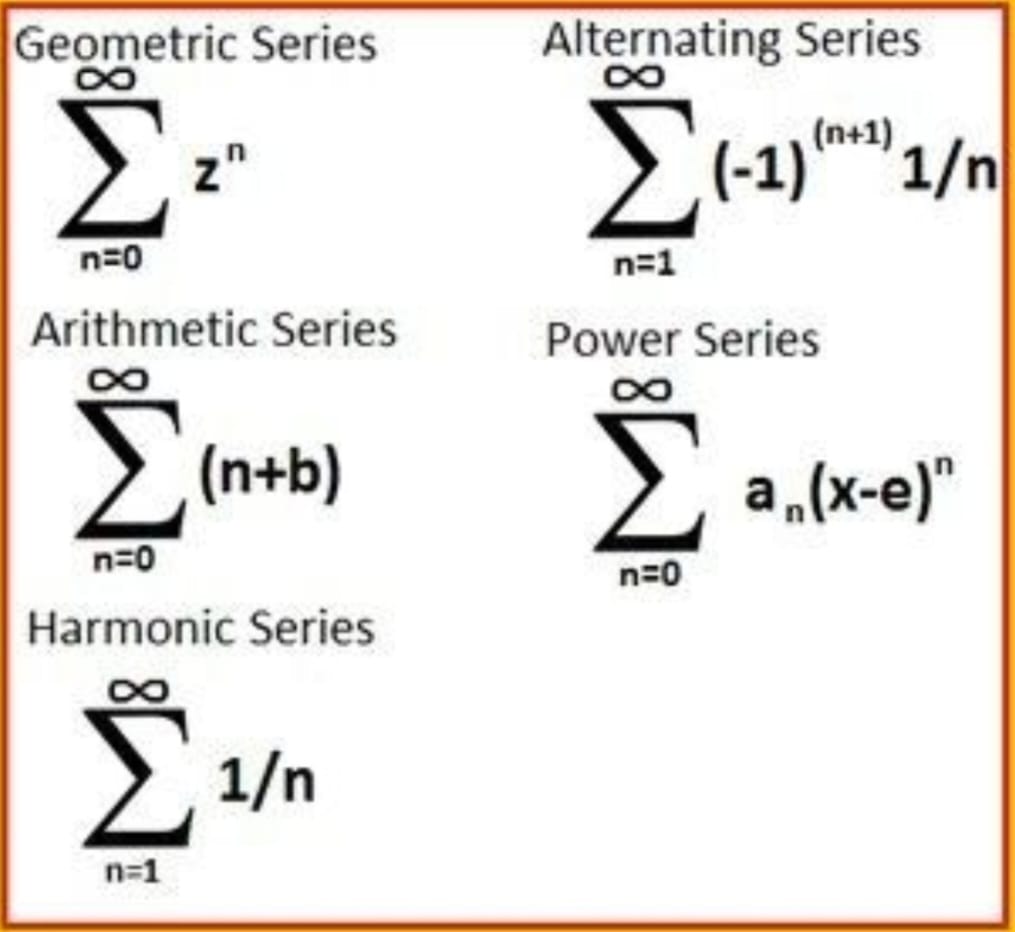
noun: (mathematics) the sum of a finite or infinite sequence of expressions
noun: a periodical that appears at scheduled times
noun: (sports) several contests played successively by the same teams ("The visiting team swept the series")
noun: similar things placed in order or happening one after another ("They were investigating a series of bank robberies")
noun: a group of postage stamps having a common theme or a group of coins or currency selected as a group for study or collection ("The Post Office issued a series commemorating famous American entertainers")
noun: (electronics) connection of components in such a manner that current flows first through one and then through the other ("The voltage divider consisted of a series of fixed resistors")
noun: a serialized set of programs
Keely
"Given that force can be exerted by an act of will, do we understand the mechanism by which this is done? And if there is a gap in our knowledge between the conscious idea of a motion and the liberation of muscular energy needed to accomplish it, how do we know that a body may not be moved without ordinary material contact by an act of will? Keely contends that all metallic substances after having been subjected to a certain order of vibration may be so moved. "Scientists are verging rapidly toward the idea that immense volumes of energy exist in all conditions of corpuscular space. I accept Prof. Stoney's idea that an apsidal motion might be caused by an interaction between high and low tenuous matter, but such conditions, even of the highest accelerated motion are too far down below the etheric realm to influence it sympathetically, even in the most remote way. The conception of the molecule disturbing the ether, by electrical discharge from its parts is not correct... the highest conditions associated with electricity come under the fourth descending order of sympathetic conditions. The conjecture as regards the motion being a series) of harmonic elliptic ones, accompanied by a slow apsidal one, I believe to be correct... The combination of these motions would necessarily produce two circular motions of different amplitudes whose differing periods might correspond to two lines of the spectrum as conjectured, and lead the experimenter, perhaps, into a position corresponding to an ocular illusion. Every line of the spectrum, I think, consists not of two close lines, but of compound triple lines; though not until an instrument has been constructed, which is as perfect in its parts as is the sympathetic field that environs matter, can any truthful conclusion be arrived at from demonstration." [Keely] [FORCE - Snell]
Russell
"Creation is but a swing of the cosmic pendulum from inertia, through energy, and back again to inertia, forever and forever. It is but a series of opposing pulsations of action and reaction, integration and disintegration, gravitation and radiation, appearance and disappearance." [The Cosmic Pendulum]
Hughes
The twelve major scales
—The term key-note employed in the ordinary sense of the musician
—The twelve key-notes, with the six notes of each as they veer round in trinities, are written in musical clef, and the scales added
—The reversal of the four and three of the key-note and its trinities in the seven of its scale
—The twelve keys follow each other seven times through seven octaves linked into the lower and higher series
—Keys mingled
—The modulating of scales, the eleventh notes rising to higher keys, . . . . . . 26 [Harmonies of Tones and Colours, Table of Contents2 - Harmonies]
The modulating gamut
—One series of the twelve keys meeting by fifths through seven octaves
—Keys not mingled
—A table of the key-notes and their trinities thus meeting
—The fourths not isolated
—The table of the twelve scales meeting by fifths
—The twelve keys, trinities, scales, and chords thus meeting are written in musical clef
—The twelve meeting through seven circles, each circle representing the eighteen tones
—The keys of C and G meeting, coloured
—Retrospection of the various major developments, . . . . 29 [Harmonies of Tones and Colours, Table of Contents3 - Harmonies]
The twelve keys meeting by fifths, one series modulating through seven octaves, keys not mingled
—The twelve veering round, the intermediate notes not coloured
—The keys of A and E meeting the intermediate notes coloured in musical clef, . . . . . 39 [Harmonies of Tones and Colours, Table of Contents3 - Harmonies]
The twelve major and the twelve minor keys written in musical clef
—First, the twelve major keys rising mingled as they develope seven times through seven octaves
—Second, one series of the twelve meeting by fifths, keys not mingled
—Third, the twelve minor keys mingled
—Fourth, the twelve minor key-notes and their trinities, the keys meeting by fifths in the line above the keys of the ascending scales, and in the line below the keys of the descending scales, 42 [Harmonies of Tones and Colours, Table of Contents3 - Harmonies]
I had for a long time studied the development of the harmonics of colour, and believed that I had gained them correctly; but I saw no way of proving this. The thought occurred—Why not test the laws in musical harmonies? I wrote down the development of the seven major keys of the white notes in keyed instruments. I was perplexed by the movement as of "to and fro," but the development of numbers explained this point, and I found that the method of development in colours, tones, and numbers agreed. I remembered the keys with sharps, but had forgotten that B? belonged to the key of F, and here I thought that the laws failed. But I found by reference that all were correct, the eighth being the first of a higher series, the laws having enabled me to distinguish between flats and sharps, [Harmonies of Tones and Colours, General Remarks on Harmonies of Tones and Colours, page 12]
whether veering round, or advancing and retreating in musical clef. I next tried the major keys which develope flats, and I thought that G? would develope a perfect harmony, but found that it must be F#, and that in this one harmony E# must be used in place of F?; on reference, I found that thus the twelve keys developed correctly in succession, the thirteenth being the octave, or first of a higher series. [Harmonies of Tones and Colours, Dr. Gauntletts Remarks1, page 13]
Of course, true Art cannot be opposed to Nature, although all the rules of the musician are not the facts of Nature. Music, pure, natural, and harmonical, in the true and evident sense of the term, is the division of any key-note, or starting-point, into its integral and ultimate parts, and the descending divisions will always answer to the ascending, having reference to a general whole. The essence and mystery in the development of harmonies consist in the fact that every key-note, or unit, is a nucleus including the past, the present, and the future, having in itself an inherent power, with a tendency to expand and contract. In the natural system, as each series rises, its contents expand and fall back to the original limit from any point ascending or descending; we cannot perceive finality in any ultimate; every tone is related to higher and lower tones, and must be a part of an organised whole. It is well known how deeply the late Sir John Herschel studied this subject; and it was his opinion that there was some principle in the science of music which had yet to be discovered.[Harmonies of Tones and Colours, The Method of Development or Creation of Harmonies2, page 16]
If the laws which I shall endeavour to explain develope the twelve major harmonies, with each note in succession expanding its six tones from within itself; and if each of these is found to be a lower development, which leads the ear to a corresponding higher expansion of the twelve major key-notes, and the six tones of each ascending and descending in an unbroken sequence from any twelve consecutively, the thirteenth being the octave of the first, which commences a higher or a lower series; and if the twelve minor harmonies are also gained by the same laws from their twelve relative key-notes (the thirteenth again being octave): if, again, all other notes are shown to be but higher or lower repetitions of these twenty-four harmonies—may we not consider the problem as in some measure solved? especially as the harmonies proceed in geometric as well as harmonical ratio, and an accurate parallel can be traced between the development of notes and colours, which latter correspond with all the intricacies of harmonic sounds. [Harmonies of Tones and Colours, The Method of Development or Creation of Harmonies3, page 17]
In the diagrams the circles are not drawn as interlacing into each other, from the difficulty of representing them accurately as rising spirally in geometric progression. If we endeavour to realise the development of harmonies, both in geometric order, and at the same time advancing and retiring, as in musical clef, we must imagine a musician having the physical power of striking all the notes on a circular keyed instrument of seven octaves, linked to a lower series of seven octaves, and a corresponding series of seven higher. But in fact the depth of the lower series, and the height of the higher, are alike unfathomable to our present powers. C, the first note of the seven octaves, sounds the four lowest tones, F, G, A, B of the lower series; and B, the last and highest note of the seven octaves, sounds in its harmony C? and D# of the higher series of sevens. [Harmonies of Tones and Colours, The Method of Development or Creation of Harmonies3, page 17]
suspected. Let us take as our standard of colours the series given by the disintegration of white light, the so-called spectrum: as our standard of musical notes, let us take the natural or diatonic scale. We may justly compare the two, for the former embraces all possible gradations of simple colours, and the latter a similar gradation of notes of varying pitch. Further, the succession of colours in the spectrum is perfectly harmonious to the eye. Their invariable order is— red, orange, yellow, green, blue, indigo, and violet; any other arrangement of the colours is less enjoyable. Likewise, the succession of notes in the scale is the most agreeable that can be found. The order is—C, D, E, F, G, A, B; any attempt to ascend or descend the entire scale by another order is disagreeable. The order of colours given in the spectrum is exactly the order of luminous wave-lengths, decreasing from red to violet. The order of notes in the scale is also exactly the order of sonorous wave-lengths, decreasing from C to B." [Harmonies of Tones and Colours, On Colours as Developed by the same Laws as Musical Harmonies2, page 19]
The inequality of the equinoctial points is a well-known fact. It will be seen how apparent this is in the developments of harmonies. From the moment that trinities depart from unity, the balance is unequal, and the repeated endeavours after closer union cause a perpetual restlessness. May not this want of equilibrium be the life or motive power of the entire universe, with its continuous struggle after concord, even to oneness? "Closer and closer union is the soul of perfect harmony." In tracing harmonies of tones and colours, the double tones of keyed instruments will be seen to correspond with the intermediate tints and shades of colours. The twelve notes, scales, and chords in the major and minor series, the meetings by fifths, &c., all agree so exactly in their mode of development, that if a piece of music is written correctly in colours with the intermediate tints and shades, the experienced musician can, as a rule, detect errors more quickly and surely with the eye than the ear, and the correct eye, even of a non-musical person, may detect technical errors. Although the arithmetical relation has been most useful in gaining the laws, it is not here entered upon; but numbers equally meet all the intricacies both of tones and colours. The bass notes have been omitted, in order to simplify the scheme. [Harmonies of Tones and Colours, The Arabian System of Music, page 21]
The diagram begins with C, the third space of the treble clef, as being more convenient to write than C, the lowest note in the bass clef. The life of musical sounds rising from a hidden fountain of life is shown by the chasms of keyed instruments between B and C, and E and F; their great use will be strikingly manifest as the developments proceed. The fundamental key-note C and its root F rise from the chasms. B, the twelfth key-note, and E, its root, sound the octave higher of the fountain B. The generation of harmonies is by one law a simple mode of difference. Each major major key-note and its tones embrace the eighteen tones of keyed instruments which all lie in order for use. The power and extent of each are complete in itself, rising and developing, not from any inherent property in matter, but from the life communicated to matter. In the whole process of harmony there are limits, and yet it is illimitable. Its laws compel each key-note to follow certain rules within certain bounds; each separate key-note, being the fountain of its own system, has its own point of rest, and series after series rise and enlarge, or fall and diminish infinitely. [Harmonies of Tones and Colours, Diagram I - The Eighteen Tones of Keyed Instruments, page 22a]
A key-note developing its harmony may be compared to a seed striking its root downwards, and rising upwards. On striking a note, it sounds from within itself, in a rapid and subdued manner, the six kindred tones necessary to its harmony, and all which do not belong to that individual harmony are kept under; thus all harmonies are in sevens. Each seven forms an ascending and descending series; the ear is aware of the tones, but not of the order in which they rise. [Harmonies of Tones and Colours, Diagram II - The Twelve Keynotes1, page 23]
This diagram represents the two last major primaries of a series of 12; 12 of a higher series follow, and the two first of a still higher series: the secondaries are written below the primaries, the sharps or flats belonging to the different harmonies are written to each note. Each primary sounds the same tones as the secondaries of each third harmony below, but in a different order; and the double tones are altered sharp or flat as the harmonies require.
By reference to previous coloured notes it will be seen that all these agree. [Harmonies of Tones and Colours, The Two Last Major Primaries, page 24e]
In the progression of harmonies these are always closely linked into each other. If any key-note is taken as central, its root will be the fifth note of its harmony below, and it becomes in its turn the root of the fifth note above. If we add the silent notes, the root of the central note is the eighth below, and becomes the root of the eighth above. To explain the lower series of the notes sounding the six tones from within themselves, the only plan appeared to be to write the tones as notes in musical clef. By reference to Chapter V., we see that the lowest series still sound their tones, and lead the ear to the higher series of a key-note, and the six notes of its harmony, as they follow each other in trinities. [Harmonies of Tones and Colours, Diagram III - The Major Keynotes Developing by Sevens, page 25a]
The twelve key-notes, with the six notes of each as they veer round in trinities, are again written in musical clef, and the scales added. The key-note leads the scale, and, after striking the two next highest notes of the seven of the harmony, goes forward, with its four lowest, an octave higher. The seven of each harmony have been traced as the three lowest, thus meeting the three highest in three pairs, the fourth note being isolated. Notwithstanding the curious reversal of the three and four of the scale, the three lowest pair with the three highest, and the fourth with its octave. The four pairs are written at the end of each line, and it will be seen how exactly they all agree in their mode of development. Keys with sharps and keys with flats are all mingled in twelve successive notes. If we strike the twelve scales ascending as they follow each other, each thirteenth note being octave of the first note of the twelve that have developed, and first of the rising series, the seventh time the scales gradually rise into the higher series of seven octaves beyond the power of the instrument. Descending is ascending reversed. After the seven and octave of a scale have been sounded ascending, the ear seems to lead to the descending; but ten notes of any scale may be struck without the necessity of modulation; at the seventh note we find that the eleventh note in the progression of harmonics rises to meet the seventh. For instance, B, the seventh note in the scale of C, must have F#. This point will be fully entered into when examining the meeting of fifths. To trace the scale of C veering round as an example for all, we may begin with C in Diagram II., and go forward with F, G, A, and B an octave higher. If the twelve scales were traced veering round, they would be found to correspond with the twelve as written in musical clef. [Harmonies of Tones and Colours, Diagram IV - The Development of the Twelve Major Scales, page 26a]
IF we strike the twelve keys of harmonies in trinities, scales, and chords, as written in musical clef, beginning with the lowest C in the bass clef, this first development is linked into the lower series of seven octaves by the four lower tones sounded by C. If we follow with the twelve keys six times, at the seventh time they will gradually rise into the higher series. We obtain a glimpse of the beauty arising from musical notes in the Pendulograph. How exquisite would they be if they could be represented in their natural coloured tones! — as, for instance, the chord of the scale of C in red, yellow, and blue, with the six coloured tones rising from each, and harmoniously blended into each other. [Harmonies of Tones and Colours, The Twelve Keys Rising Seven Times, page 28a]
THE twelve keys have been traced following each other seven times through seven octaves, the keys mingled, the thirteenth note being the octave, and becoming first of each rising twelve. Thus developing, the seven notes of each eighth key were complementary pairs, with the seven notes of each eighth key below, and one series of the twelve keys may be traced, all meeting in succession, not mingled. When the notes not required for each of the twelve thus meeting are kept under, the eighths of the twelve all meet by fifths, and as before, in succession, each key increases by one sharp, the keys with flats following, each decreasing by one flat; after this, the octave of the first C would follow and begin a higher series. It is most interesting to trace the fourths, no longer isolated, but meeting each other, having risen through the progression of the keys to higher harmonies. In the seven of C, B is the isolated fourth, meeting F#, the isolated fourth in the key of G, and so on. Each ascending key-note becomes the root of the fifth key-note higher; thus C becomes the root of G, &c. [Harmonies of Tones and Colours, Diagram VII - The Modulating Gamut of the Twelve Keys1, page 29]
Finally, trace the twelve keys by fifths as they veer round through the seven circles, each circle representing the eighteen tones. Beginning with C in the innermost circle ascending, C becomes the root of G, G of D, and so on. In descending, begin with C in the outermost circle (though really the first of a higher series which we have not the power of striking on instruments); F, its root, becomes the key-note, B? the root and then the key-note, and so on. The keys thus gained are written in musical clef below. [Harmonies of Tones and Colours, The Twelve Scales Meeting by Fifths, page 31a]
The keys of C and G meeting are coloured, and show the beautiful results of colours arising from gradual progression when meeting by fifths. Each key-note and its trinities have been traced as complete in itself, and all knit into each other, the seven of each rising a tone and developing seven times through seven octaves, the keys mingled. The twelve scales have been traced, developing seven times through seven octaves, all knit into each other and into the key-notes and their trinities. The chords have also been traced, each complete in itself, and all knit into each other and into the key-notes, trinities, and scales. And lastly, one series of the twelve keys, no longer mingled, but modulating into each other, have been traced, closely linked into each other by fifths through seven octaves, three keys always meeting. Mark the number of notes thus linked together, and endeavour to imagine this number of tones meeting from the various notes. [Harmonies of Tones and Colours, The Twelve Scales Meeting by Fifths, page 31a]
Probably the lowest harmony which we have the power of partially hearing is A minor, rising in the lower series of seven octaves; C, its highest note, sounding the six tones of C, its major harmony, on our horizon of sound. The diagram begins with A, the second space of the treble clef, as most convenient for writing. [Harmonies of Tones and Colours, The Minor Harmonies, page 33a]
This diagram shews the two last minor primaries of a series of 12, with the 12 of a higher series, and the two first of a series higher still. As in the diagram of the Major, the secondaries are written below the primaries, and the sharps or flats of each harmony are written to their respective notes. With the exception that one of the primaries rises a tone higher, it will be observed that in the same way the notes of each minor primary are identical with the secondaries of each third harmony below, but in a different order; and the double tones are altered sharp or flat, as before. [Harmonies of Tones and Colours, Diagram Shews the Two Last Primaries, page 34e]
THE same laws are followed here as in the development of the major scales. In that of A, F, the sixth note, has risen to F#, in order to meet B, which has previously sounded. In descending, the seventh note, B, falls to B?, in order to meet F, which has also previously sounded. The notes, ascending or descending, always follow the harmony of their key-note, except when rising higher or falling lower to meet in fifths. We may here trace the twelve, the ascending scale sounding the fifth harmony higher than its key-note, and, in descending, sounding the fifth lower harmony. The four pairs of each scale are written at the end of the lines. If we strike the twelve scales as they follow in succession, the thirteenth note being the octave of the first, and leader of a higher twelve; having gained them six times, at the seventh they gradually rise (though beyond the power of a keyed instrument) into the higher series of seven octaves, and again, in descending, they fall lower, and are linked into the lower series of seven octaves. Nine notes of any ascending minor scale may be struck without the necessity of modulating beyond the fifth harmony. For example, in the scale of A, its tenth note, C#, rises to meet the sixth note, which has previously sounded. In descending, E?, the eleventh note, meets B?, the seventh note, which has previously sounded. The scale of A may be traced veering round by reference to Diagram IX., beginning with A, and carrying the four lowest notes an octave higher, F rising to F# in ascending, B falling to B? in descending. [Harmonies of Tones and Colours, Diagram XI - The Twelve Minor Keynotes with the Six Note of Each, page 36a]
Lastly, we trace the twelve ascending by fifths as they veer round through the seven circles, each circle representing the eighteen tones, beginning with A in the innermost circle. A becomes the root of E, E of B, and so on. In descending, we begin with A in the outermost circle, though it is in fact the commencement of a higher series which we cannot strike. D, its root, becomes the fifth key-note lower, and so on. The keys of A and E are coloured, to show the result of the minor harmonies meeting by fifths. [Harmonies of Tones and Colours, Diagram XIV - The Modulating Gamut of the Twelve Minor Keys by Fifths3, page 41a]
TO recapitulate from the beginning, observe, firstly, the twelve major key-notes as they have developed from within themselves in succession, six tones in trinities seven times through seven octaves, each thirteenth note being the octave of the first note of the twelve that have developed, and being also the first of the higher series. We may retrace all as still sounding their tones, the key-notes leading the ear to the six notes of each harmony, the keys with sharps and those with flats being mingled. The ascending and descending scales always agree in their harmonies with the key-notes and their trinities. [Harmonies of Tones and Colours, Diagram XV - The Twelve Major and the Twelve Minor Keys, page 42a]
Secondly, we have the one series of the twelve keys as they meet by fifths through the seven octaves. The keys are no longer mingled; the scales meet by fifths in the same keys and their trinities. [Harmonies of Tones and Colours, Diagram XV - The Twelve Major and the Twelve Minor Keys, page 42a]
Thirdly, the twelve minor keys as they develope in succession seven times through seven octaves, always sounding their major harmony in trinities, and, as with the majors, each thirteenth note being the octave of the first note of the twelve, and first of the following series, the keys all mingled. [Harmonies of Tones and Colours, Diagram XV - The Twelve Major and the Twelve Minor Keys, page 42a]
Fourthly, we have one series of the seven of each of the twelve minor keys meeting by fifths through seven octaves. The keys of the twelve ascending scales are written in musical clef above the former, and the keys of the descending scales below. The ascending scales sound the fifth higher harmonies than the key-notes and their trinities, and the lower scales the fifth harmony lower than the key-notes and their trinities. The three series follow out their keys in three successive series, and all meet by fifths. [Harmonies of Tones and Colours, Diagram XV - The Twelve Major and the Twelve Minor Keys, page 42a]
See Also
9.8 - Spontaneous Creation of Harmonic Series
Electromotive Series
Fibonacci Series
Figure 9.10 - Phases of a Wave as series of Expansions and Contractions
Figure 9.5 - Phases of a Wave as series of Expansions and Contractions
Galvanic Series
Harmonic Series
Helmholtz Subharmonic Series
major series
mathematical series of notes
minor series
Overtone series
Progressive Evolution
progressive series
Sequence
series of fifths
series of numbers
series of points in space which form a shaft
series of six tones
series of twelve
Three series
transuranium series
Triboelectric series
