Sympathetic Vibratory Physics

Strictly speaking a doubling (octave) or halving of a frequency. Harmonics as used throughout SVP may include derived or developed partials not divisible by two. Also called "affiliated sounds."

(click to enlarge)

Ramsay
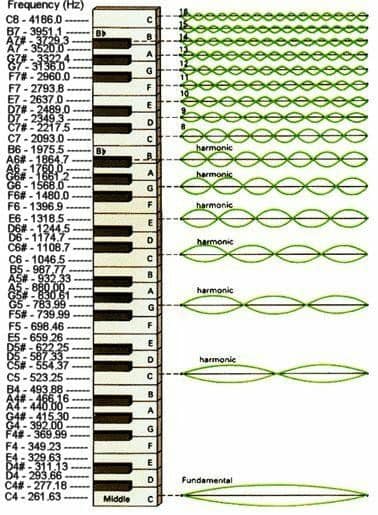
After vibrations the next thing is musical notes, the sounds produced by the vibrations falling into the ear. Sounds arise in association. There are no bare simple sounds in music; it is a thing full of the play of sympathy. Such a thing as a simple solitary sound would be felt as a strange thing in our ears, accustomed as we are to hear affiliated sounds only. These affiliated sounds, called "harmonics," or "partials" as they have also been called, because they are the parts of which the sound is made up, are like perspective in vision. In perspective the objects lying in the line of sight, seem smaller and smaller, and more dim and indefinite as they stretch away into the distance; while nearer objects and those in the foreground are apparently larger, and are more clearly seen. This is the way of a musical sound; one of its component elements, the fundamental partial, being, as it were, in the foreground to the ear, is large and pronounced; while the other elements are less distinctly heard, and are fainter and fainter as they recede into the musical distance in the perspective of the ear. Few have any idea of the number of these weaker partials of a musical sound. Tyndal's illustrations in his very instructive work on Sound show a string spontaneously divided into twenty segments, all vibrating separately, being divided by still nodes along its length; and a vibrating string will keep thus [Scientific Basis and Build of Music, page 58]

dividing itself by 2 or 3 or 5, etc., up through the whole geometrical series of numbers, not keeping fixed at one thing; but while the whole length is vibrating the fundamental partial, it keeps shifting the still nodes along its length, and sometimes longer and sometimes shorter segments are sounding the other partials which clothe the chief sound. It has been commonly said that "a musical sound is composed of three sounds," for every ear is capable of hearing these three, and with a little attention a few more than these; but many will be startled when told that there are twenty-five sounds in that sound. Eighteen of them are simply the octaves of the other seven, all of these seven except one having one or more octaves in the sound. Four of the seven also are very feeble, the one which has no octave being the feeblest of all. Two of the other three are so distinctly audible along with the chief partial that they gave rise to the saying we have quoted about a musical sound being composed of three sounds.¹ If the three most pronounced partials were equally developed in one sound, it could not be called one sound - it would decidedly be a chord; and when in the system they do become developed, they form a chord; but in the one sound they, the partials, having fewer and fewer octaves to strengthen them, fade away in the perspective of sound. The sharp seventh, which in the developed system has only one place, not coming into existence until the sixth octave of the genesis, is by far the feeblest of all the partials, and Nature did well to appoint it so. These harmonics are also sometimes called "overtones," because they are higher than the fundamental one, which is the sound among the sounds, as the Bible is the book among books. [Scientific Basis and Build of Music, page 59]

Partials - Harmonics, so called because they are the parts of a sound. [Scientific Basis and Build of Music, page 63]

Helmholtz falls into a mistake when he says- "The system of scales and modes, and all the network of harmony founded on them, do not seem to rest on any immutable laws of Nature, but are due to the aesthetical principle which is constantly subject to change, according to the progressive development of taste." It is true, indeed, that the ear is the last judge; but the ear is to judge something which it does not create, but simply judges. Nature is the maker of music in its scales and modes. The styles of composition may vary with successive generations, and in the different nations of men; but the scientific basis of music is another thing. It is a thing, belonging to the aesthetic element of our being and our environment; it is under the idea of the beautiful, rather than the idea of the useful or the just; but all these various aspects of our relation to creation have their laws which underlie whatever changes may be fashionable at any period in our practice. If the clang-farbe of a musical tone, that is, its quality or timbre, depends on the number and comparative strength of the partial tones or harmonics of which it is composed, and this is considered to be the great discovery of Helmholtz, it cannot be that the scales and modes are at the caprice of the fickle and varied taste of times and individuals, for these partials are under Nature's mathematical usages, and quite beyond any taste for man's to change. It is these very partials or harmonics brought fully into view as a system, and they lead us back and back till they have brought us to the great all-prevading law of gravitation; it is these very partials, which clothe as an audible halo every musical sound, which constitute the musical system of sounds. [Scientific Basis and Build of Music, page 78]

The sympathy of one thing with another, and of one part of a thing with another part of it, arises from the principle of unity. For example, a string requires to be uniform and homogenous to have harmonics producing a fine quality of tone by the sweet blendings of sympathy; if it be not so, the tone may be miserable ... You say you wish I were in touch with Mr. Keely; so do I myself ... I look upon numbers very much as being the language which tells out the doings of Nature. Mr. Keely begins with sounds, whose vibrations can be known and registered. I presume that the laws of ratio, position, duality, and continuity, all the laws which go to mould the plastic air by elastic bodies into the sweetness of music, as we find them operative in the low silence of oscillating pendulums, will also be found ruling and determining all in the high silence of interior vibrations which hold together or shake asunder the combinations which we call atoms and ultimate elements, but which may really be buildings of wondrous complexity occupying different ranges of place and purpose between the visible cosmos and Him who built and evermore buildeth all things. The same laws, though operating in different spheres, make the likenesses of things in motion greater than the differences. [Scientific Basis and Build of Music, page 87]

HARMONICS ON THE VIOLIN.

At the middle of the string the stopped note and the harmonic notes are the same; but corresponding places above and below the middle give the same harmonic, although these places when stopped give different notes. [Scientific Basis and Build of Music, page 92]

When Ramsay gave a course of lectures in Glasgow, setting forth "What constitutes the Science of Music," his lecture-room was hung round with great diagrams illustrating in various ways his findings; an ocular demonstration was also given of the system of musical vibrations by his favorite illustration, the oscillations of the Silent Harp of Pendulums. A celebrated teacher of music in the city came to Mr. Ramsay's opening lecture, and at the close remained to examine the diagrams, and question the lecturer, especially on his extension of the harmonics to six octaves. Having seen and heard, this teacher went and shortly after published it without any acknowledgment of the true authorship; and it was afterwards republished in some of the Sol-Fa publications, the true source unconfessed; but our plagarist stopped short at C, the top of the tonic, instead of going on to F, the sixth octave of the root of all; the effect of this was to destroy the unity of the great chord. The 22 notes instead of 25, at which this teacher stopped, allowed him, indeed, to show the natural birthplace of B, which Ramsay had pointed, but it beheaded the great complex chord and destroyed its unity. If C, the root of the tonic, be made the highest note, having quite a different character from F, it pronounces its character, and mars the unity of the great chord. Similar diversity of effect is produced by cutting off only two notes of the 25 and stopping short at D, the top of the dominant; and also, though in a weaker degree, by cutting off only one note of the 25 and stopping at E, the middle of the tonic; this, too, disturbs the unity of the fundamental sound. [Scientific Basis and Build of Music, page 111]

Hughes
On colours developing by the same laws as musical harmonies
—The physical properties of light and darkness briefly considered
—If the laws are correctly gained, harmonics of tones and of colours will agree
—Quotation from a lecture by Professor W. F. Barrett on the order of sonorous and luminous wave-lengths
—Fountain of musical harmonics, E root of B; in colours yellow and ultra-violet, being tints and shades of white and black
—All harmonics of sound and colour condense into a primo springing from the fountain
—Multequivalency of tones and colours
—Wünsch's views nearly one hundred years ago
—Clerk Maxwell's, Lord Rayleigh's, and [Harmonies of Tones and Colours, Table of Contents1 - Harmonies]

I had for a long time studied the development of the harmonics of colour, and believed that I had gained them correctly; but I saw no way of proving this. The thought occurred—Why not test the laws in musical harmonies? I wrote down the development of the seven major keys of the white notes in keyed instruments. I was perplexed by the movement as of "to and fro," but the development of numbers explained this point, and I found that the method of development in colours, tones, and numbers agreed. I remembered the keys with sharps, but had forgotten that B? belonged to the key of F, and here I thought that the laws failed. But I found by reference that all were correct, the eighth being the first of a higher series, the laws having enabled me to distinguish between flats and sharps, [Harmonies of Tones and Colours, General Remarks on Harmonies of Tones and Colours, page 12]

Sympathetic Vibratory Physics

Bridging Science and Spirituality

Search

harmonics