| Overtone Series | Overtone Series | |
Sympsionics Symbol | ||
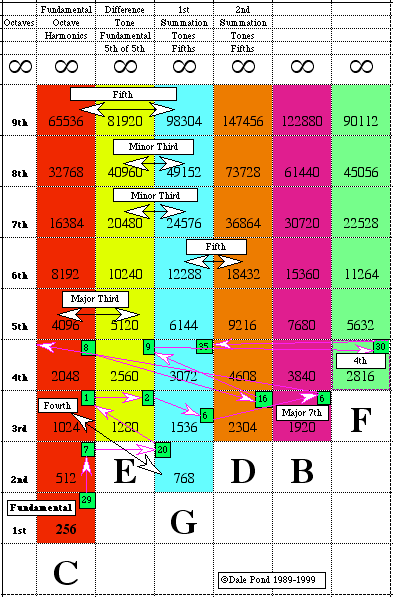
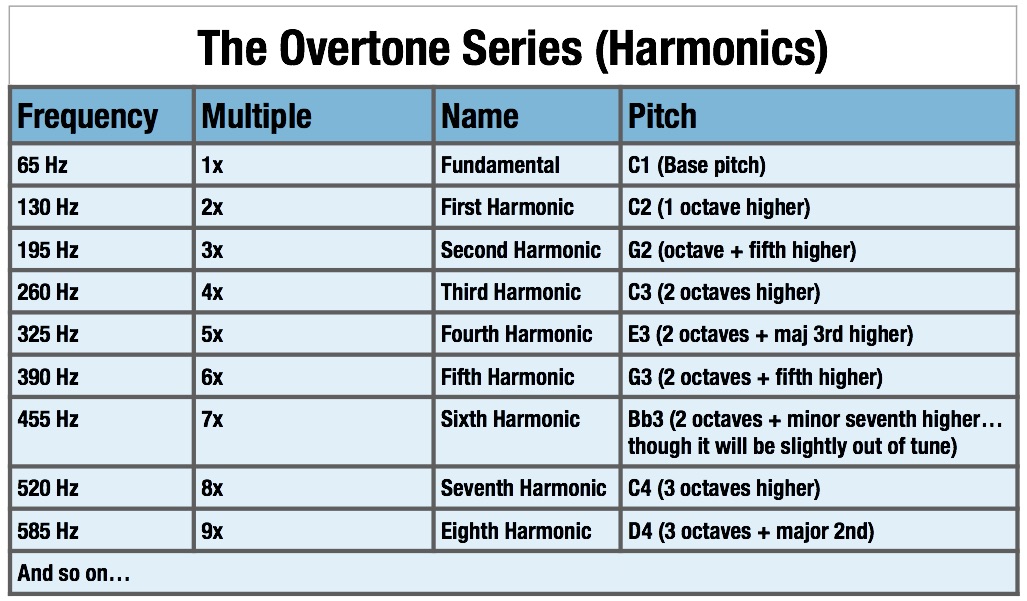
Overtone Harmonics
(See MUTATIONS for more complete list.)
C:
First Octave
1 = c
Second Octave
2 = c'
3 = g'
Third Octave
4 = c''
5 = e''
6 = g''
7 = bb (it's actually about half way between a and bb)
Fourth Octave
8 = c'''
9 = d'''
10 = e'''
11 = f#''' (halfway between f and f#)
12 = g'''
13 = a'''
14 = bb''' (sort of)
15 = b'''
16 = c
17 = c#/db
18 = d
19 = eb (a bit flatter)
20 = e
21 = ???
22 = f# (sort of)
23 = f# (a bit sharper)
24 = g
Rod Fixed at Both Ends
"A rod fixed at both ends and caused to vibrate transversely divides itself in the same manner as a string vibrating transversely.
"But the succession of its overtones is not the same as those of a string, for while the series of tones emitted by the string is expressed by the natural numbers, 1, 2, 3, 4, 5, etc., the series of tones emitted by the rod is expressed by the squares of the odd numbers, 3, 5, 7, 9, etc." [from "Sound" by John Tyndall]
Rod Fixed at One End
"A rod fixed at one end can also vibrate as a whole, or can divide itself into vibrating segments separated from each other by nodes.
"In this case the rate of vibration of the fundamental tone is to that of the first overtone as 4:25, or as the square of 2 to the square of 5. From the first division onwards the rates of vibration are proportional to the squares of the odd numbers, 3, 5, 7, 9, etc.
"With rods of different lengths the rate of vibration is inversely proportional to the square of the length of the rod." [from "Sound", John Tyndall]
Researchers discover new channels to excite magnetic waves with terahertz light
Plucking a guitar string is a simple action that generates a harmonic series of overtones. However, skilled guitar players can elevate their performance by applying pressure to the strings while plucking them. This subtle technique causes the pitch of the note to bend—rising or falling with each deft movement—and infuses the music with expressiveness, texture, and character by intentionally harnessing the “nonlinear effects” of guitar strings.
In a study published today in Nature Physics , researchers from MIT and the University of Texas at Austin draw a fascinating scientific parallel to this musical artistry. The paper, authored by MIT graduate student Zhuquan Zhang, University of Texas at Austin Postdoc Frank Gao (MIT PhD ‘22), MIT’s Haslam and Dewey Professor of Chemistry Keith Nelson, and Edoardo Baldini, an Assistant Professor of Physics at the University of Texas at Austin, demonstrates the ability to control the dancing patterns of tiny magnetic bits, often referred to as “spin waves” or “magnons,” in a nonlinear manner, akin to how skilled guitar players manipulate guitar strings. Researchers discover new channels to excite magnetic waves with terahertz light
See Also
1.20 - Evolution and Devolution of Frequency
1.23 - Power of Harmonics through Summation Tones
12.18 - Multiple Octave Progression
12.19 - Fibonacci Relationships
12.21 - Fibonacci Whole Numbers v Irrational Decimal near Equivalents
12.38 - Orbital revolution
14.15 - Movement Caused by Spirit
15.15 - Progressive Dissociation
15.15.05 - Progressive Association
3.04 - Power Accumulation via Fibonacci-like Patterns
8.17 - Law of Harmonic Vibrations
8.22 - Law of Harmonic Pitch
9.8 - Spontaneous Creation of Harmonic Series
9.9 - Sympathy or Harmony Between Harmonics or Overtones
Additive and Subtractive Synthesis
arithmetic progression
arithmetical progression
Differentiation
Dissolution
evolve
Evolution
Fibonacci Relationships
Fibonacci Series
Overtones Developed Musically
Figure 8.5 - Summation Tones
Fractal
fugue
Genesis of the Scale
Geometrical Progression
Golden Section
Growth
harmonic progression
Harmonic Series
Harmonic
Interval
Law of Harmonic Pitch
Law of Harmonic Vibrations
Life
major
major key
major scale
Master Tone
master tones
Medu-Neter
Mid-tone
Motion
Movement
musical progression
Neter
octave tones
Overtone Position
Overtone
partial
PHI
progression of adjacencies
progression of keys
Progression
Progressive Evolution
Progressive Science
Ramsay - PLATE II - The Genesis
Resultant Tone
Scale
self-evolve
Square Law
Sympathetic Vibration
Sympathy
Tetractyls
Undertone
Vibrating Rod Harmonics

