Keely describing elements of the dynasphere:
"All hollow spheres, of certain diameters, represent, as per diameters, and their volumes of molecular mass, pure, unadulterated, sympathetic resonation towards the enharmonic and diatonic thirds of any, and in fact all, concordant sounds. In tubes it is adversely different, requiring a definite number of them so graduated as to represent a confliction by thirds, sixths and ninths, as towards the harmonic scale. When the conditions are established, the acoustic result of this combination, when focalized, represents concordant harmony, as between the chord mass of the instrument to be operated and the chord mass of the tubes of resonation. Therefore the shortest way towards establishing pure concordance, between any number of resonating mediums, is by the position that Nature herself assumes in her multitudinous arrangements of the varied forms and volumes of matter - the spherical. The great difficulty to overcome, in order to get a revolution of the same sphere, exists in equating the interior adjuncts of same. In other words, the differentiation induced must be so equated as to harmonize and make their conditions purely concordant to the molecular mass of the sphere. Example: Suppose the chord of the sphere mass represents B flat, or any other chord, and the internal adjuncts by displacement of atmospheric volume differentiates the volume one-twentieth, this displacement in the shell's atmospheric volume would represent an antagonistic twentieth against the shell's mass concordance, to equate which it would be necessary to so graduate the shell's internal adjuncts as to get at the same chord; an octave or any number of octaves that comes nearest to the concordance of the shell's atmospheric volume. No intermediates between the octaves would ever reach sympathetic union.
"We will now take up the mechanical routine as associated with adjuncts of interference and follow the system for chording the mechanical aggregation in its different parts, in order to induce the transmissive sympathy necessary to perfect evolution and produce revolution of the sphere or shell.
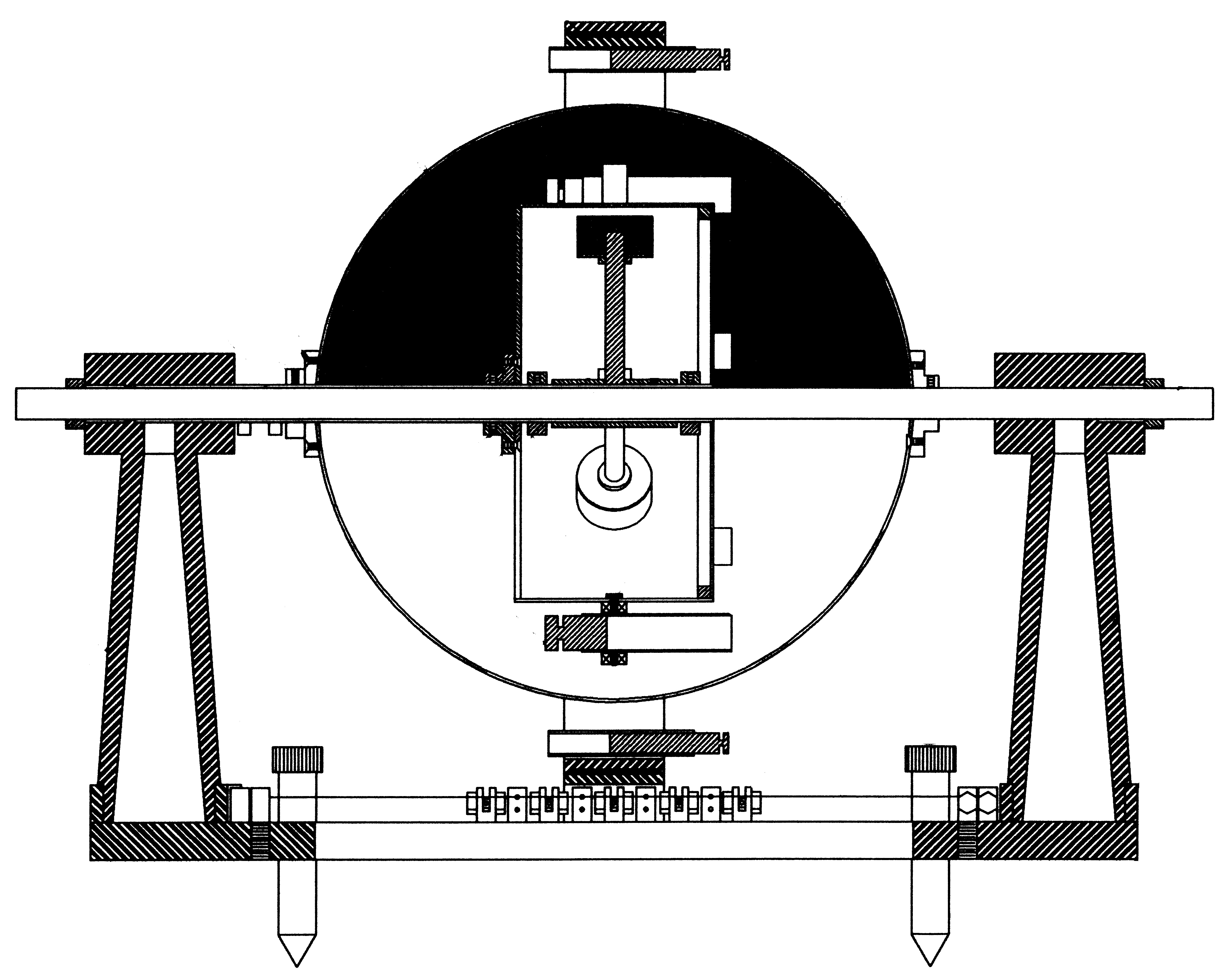
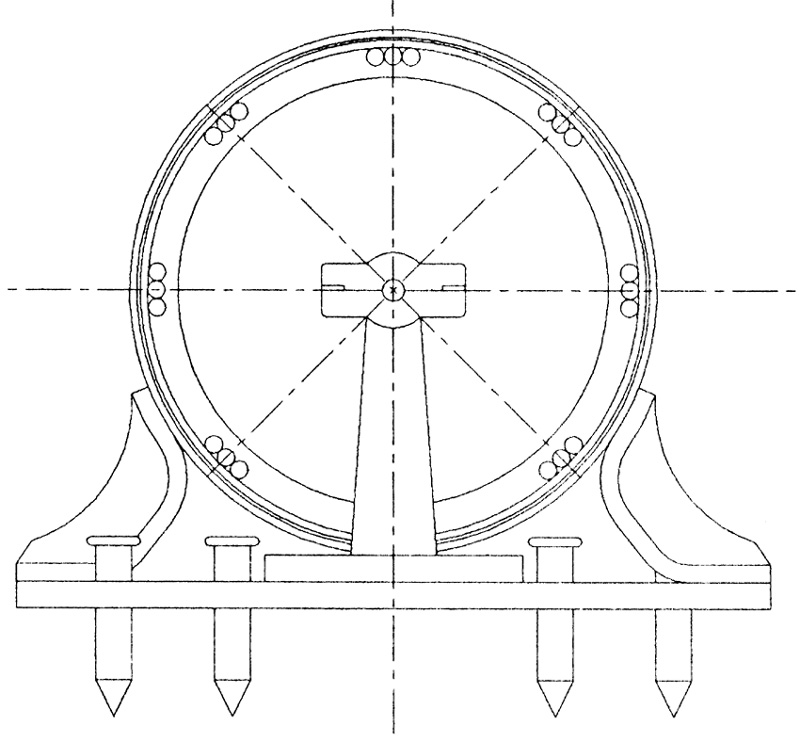
"Example: Suppose that we had just received from the machine shop a spun shell of twelve inches internal diameter, 1/32 of an inch thick, which represents an atmospheric volume of 904.77 cu. in. On determination by research we find the shell to be on its resonating volume B flat, and the molecular volume of the metal that the sphere is composed of, B natural. This or any other antagonistic chord, as between the chord mass of the shell and its atmospheric volume, would not interfere but would come under subservience. We now pass a steel shaft through its center 1/2 inch in diameter, which represents its axial rest. This shaft subjects the atmospheric volume of the shell to a certain displacement or reduction, to correct which we first register the chord note of its mass, and find it to be antagonistic to the chord mass of the shell, a certain portion of an octave. This must be corrected. The molecular volume of the shaft must be reduced in volume, either by filing or turning, so as to represent the first B flat chord that is reached by such reduction. When this is done the first line of interference is neutralized, and the condition of sympathy is as pure between the parts as it was when the globe was minus its axis. There is now introduced on its axis a ring which has seven tubes or graduating resonators, the ring being 2/3 the diameter of the globe (or 8" ID), the resonators three inches long and 3/4 in. diameter, each one to be set on the chord of B flat, which is done by sliding the small diaphragm in the tube to a point that will indicate B flat. This setting then controls the metallic displacement of the metallic combination, as also the arms necessary to hold the (inner) ring and resonators on the shaft or axis. Thus the second equation is established, both on resonation and displacement. We are now ready to introduce the diatonic scale ring (Outer Ring) of three octaves which is set at two-thirds of the scale antagonistic to the chord mass of the globe itself. This is done by graduating every third pin of its scale to B flat, thirds, which represent antagonistic thirds to the shell's molecular mass. This antagonism must be thoroughly sensitive to the chord mass of one of the hemispheres of which the globe is composed. The axis of the scale ring must rotate loosely on the globe's shaft without revolving with the globe itself, which it is prevented from doing by being weighted on one side of the ring by a small hollow brass ball, holding about two ounces of lead. The remaining work on the device is finished by painting the interior of the globe, one hemisphere black and one white, and attaching a rubber bulb such as is used to spray perfume, to the hollow end of the shaft. This bulb equates vibratory undulations, thus preventing an equation of molecular bombardment on its dark side when sympathetically influenced. It is now in condition to denote the sympathetic concordance between living physical organisms, or the receptive transmittive concordance necessary to induce rotation."

See Also
Ether
Etheric Elements
Mind in Matter
Sympathetic Flows
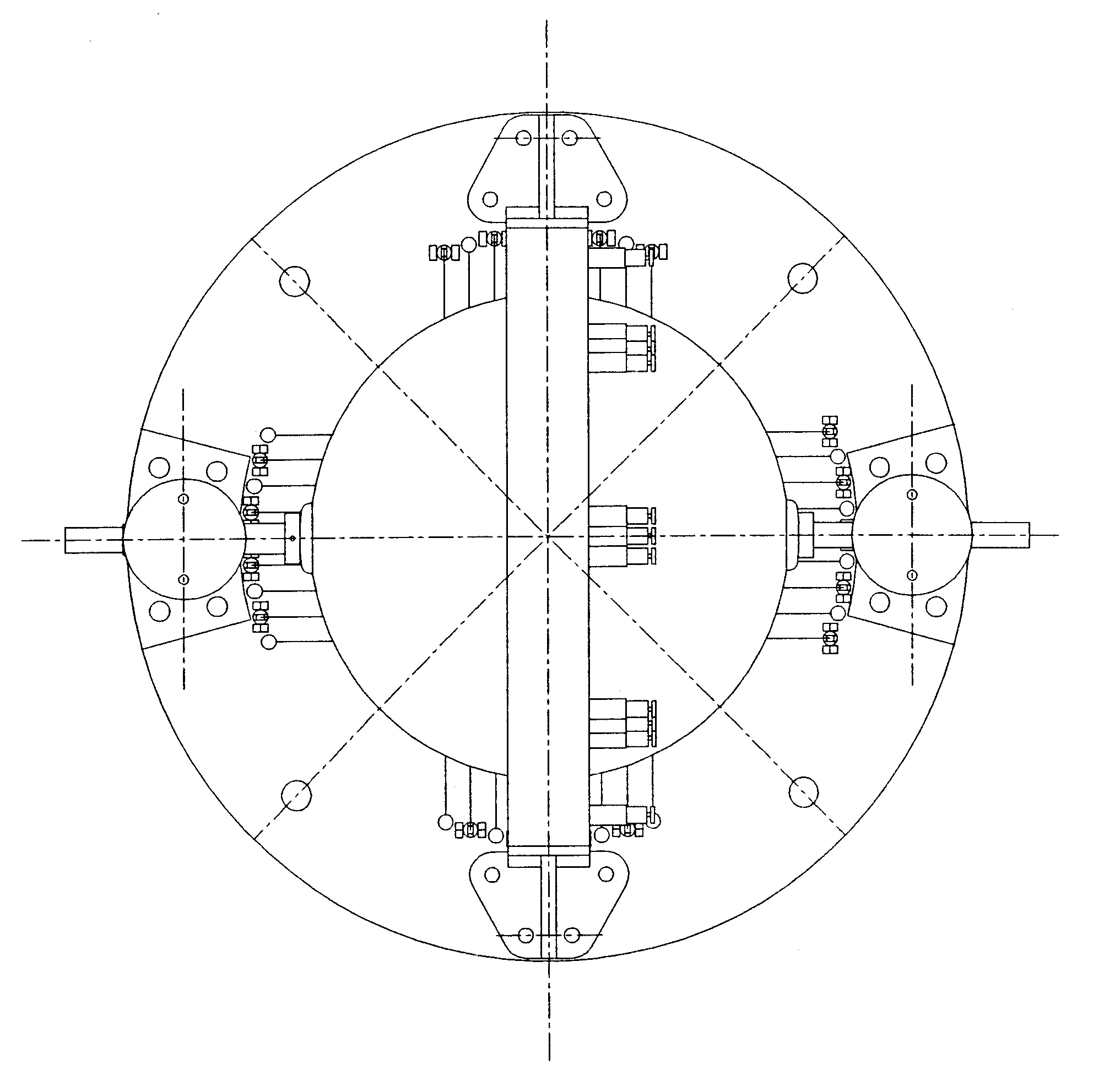
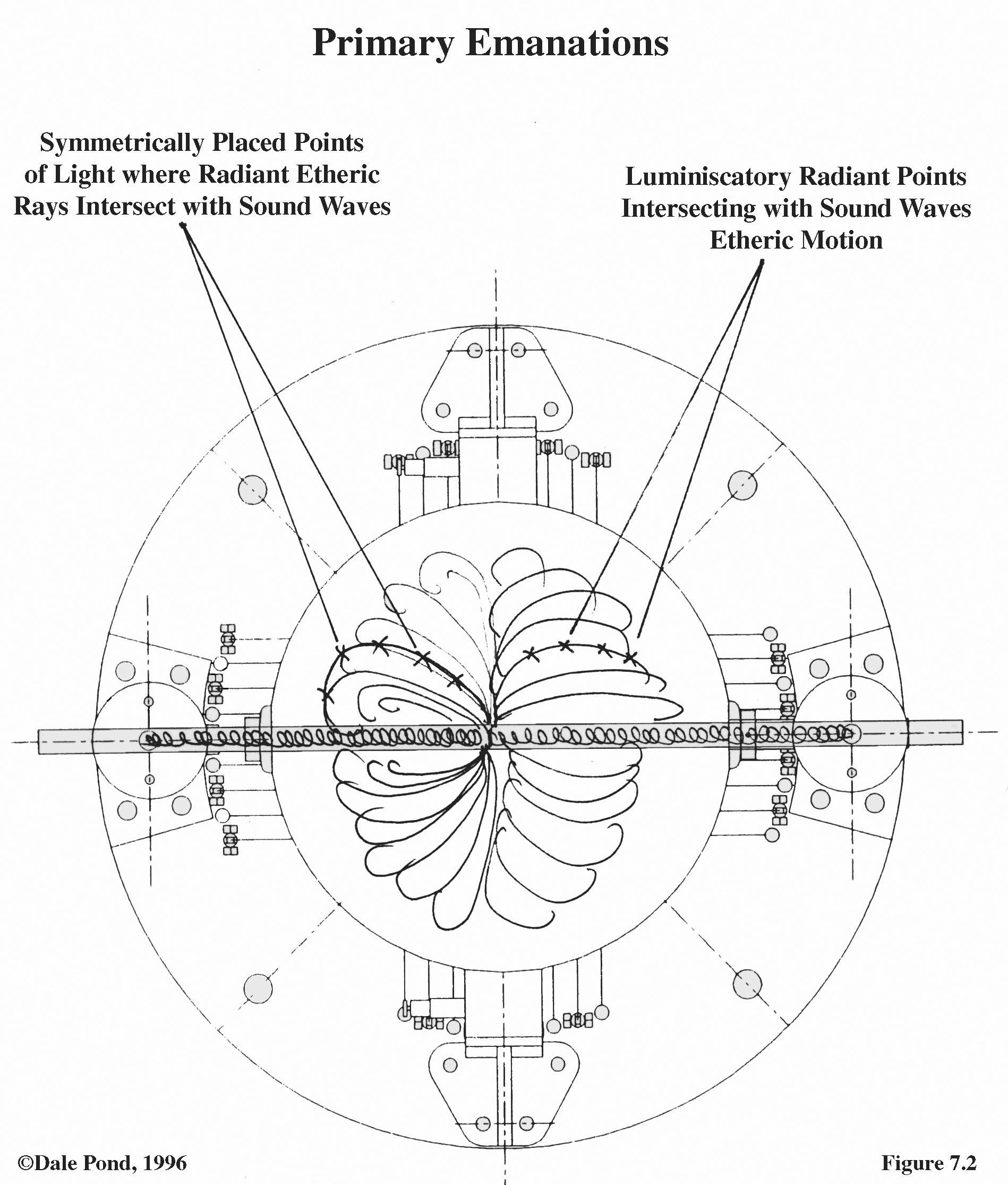
Outer Ring of Resonation
"We are now ready to introduce the diatonic scale ring (Outer Ring) of three octaves which is set at two-thirds of the scale antagonistic to the chord mass of the globe itself." Keely
Inner Ring of Resonation
"There is now introduced on its axis a ring which has seven tubes or graduating resonators, the ring being 2/3 the diameter of the globe (or 8" ID)..." Keely

See Also
diatonic scale ring
What is a Dynasphere
Dynasphere
Inner Ring of Resonation
Musical Dynasphere
Part 20 - Musical Dynasphere - Current Research
Concentric Rings
Electricity records Mind-thought in Rings of Light
Figure 14.06 - Mind and Electric Thought Rings of Motion are Closely Connected
Figure 15.06 - Thought Rings of Motion
Figure 2.1 - Mind condenses into matter via Tonal Rings between Planes
Figure 2.1.5 - Russells Rings forming Spheres from Three Pairs of Reflecting Mirrors
Light Rings formed at 90 Degrees to Magnetic Center Line
Mind Thought Rings of Motion
20.02 - Keely Describing Dynasphere Construction

Inner Ring Resonators
"a ring which has seven tubes or graduating resonators ... the resonators three inches long and 3/4 inches in diameter, each one to be set on the chord of B flat" Keely
Outer Ring Resonators
"...graduating every third pin of its scale to B flat, thirds, which represent antagonistic thirds to the shell's molecular mass." Keely
Symbol of Man
See Also
Figure 19.04 - Dynasphere Components
Chord
Dynasphere
Graduation
Scale
Figure 20.01 - Keely and his original Dynasphere circa 1889
Figure 20.02 - Dale Pond and his replica of Keelys Dynasphere 1996
18 Dynasphere Strings - https://www.svpwiki.com/Music/Strings-12-23-21.mp3
See Also
Actuator
Alcea
Altea
Alya
Atlin
Atlin - Knowing I Am
Atlin Project
chord of resonation
Dynasphere
Dynaspheric Force - Theoretical and Applied Sympathetic Vibratory Physics - Volume I
Dynaspheric Force - Theoretical and Applied Sympathetic Vibratory Physics - Volume 2
Etheric Liberator used with Atlin the Musical Dynasphere
Figure 13.23 - Three Actuators on Shaft and Black and White Coatings
Figure 20.03 - Hollow Shell 12 inches ID
Figure 20.04 - Dynasphere Components
Figure 20.05 - Primary Emanations or Energy Flows
Figure 20.06 - Side View
Figure 20.07 - Top View
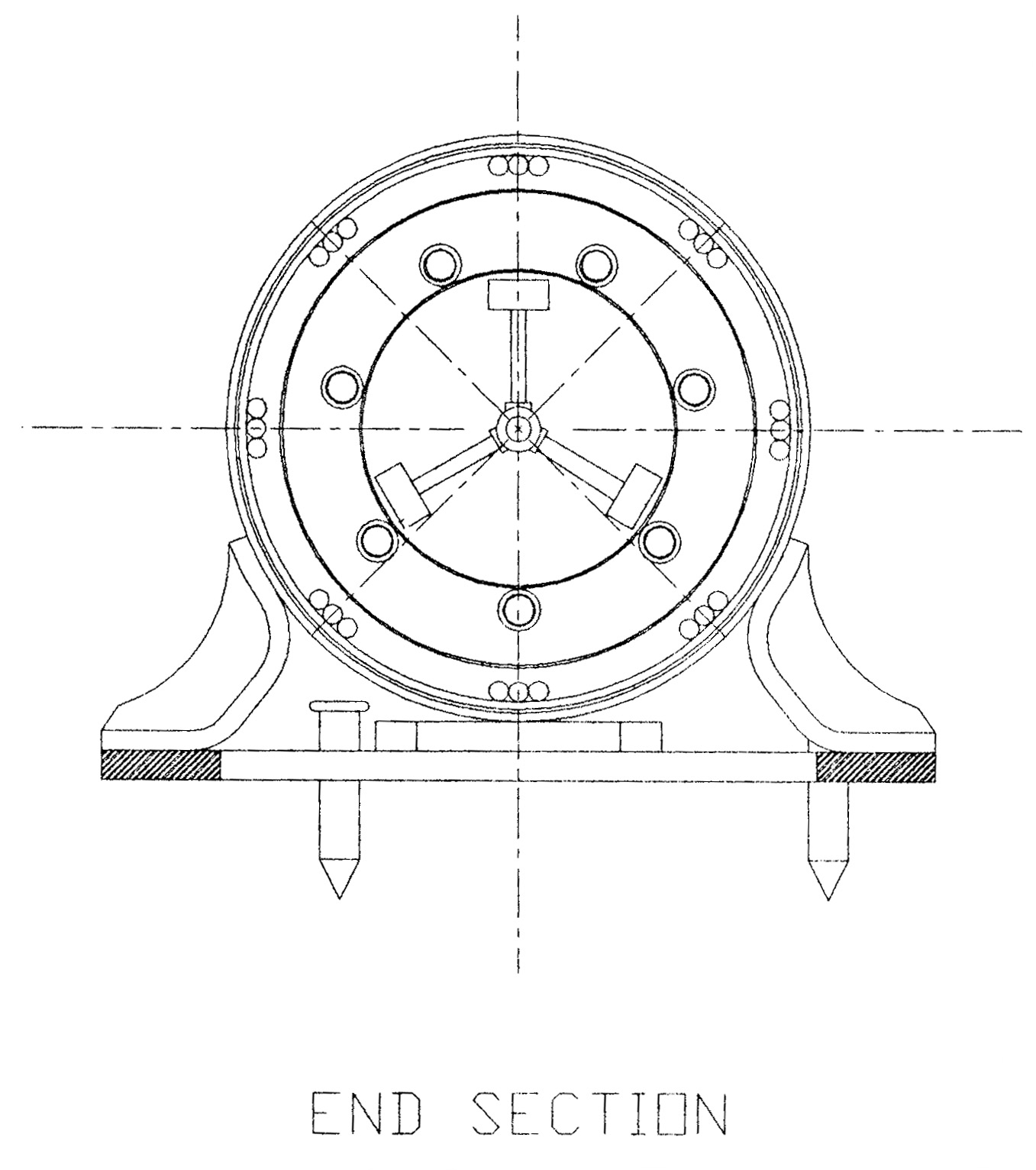
Figure 20.08 - End Elevation
Figure 20.09 - End Section View
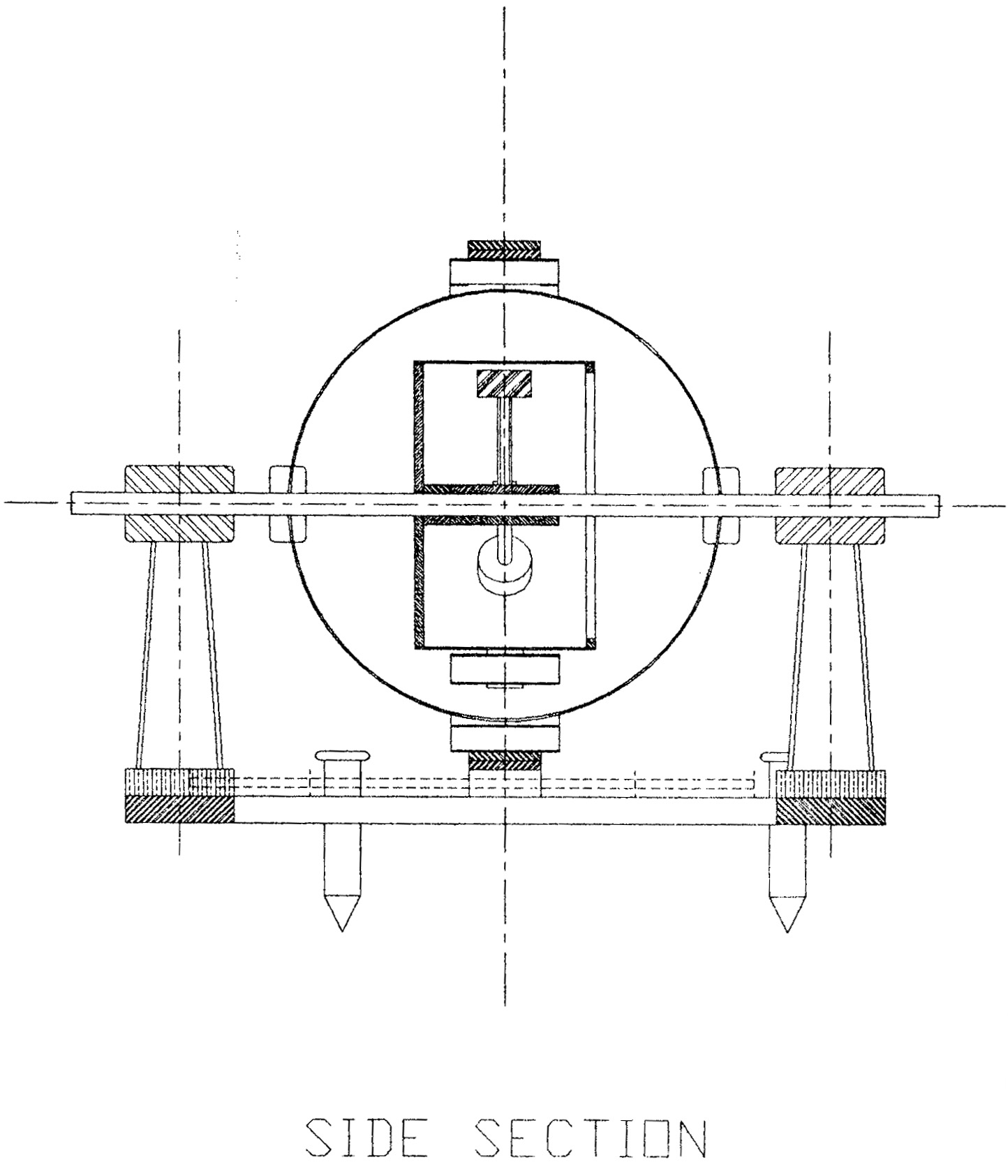
Figure 20.10 - Side Section View
Figure 20.11 - White Interior Treatment
Figure 20.12 - Black Interior Treatment
Figure 20.13 - Two Rings - Outer and Inner
Figure 20.14 - Interior View
Inner Ring of Resonation
Keely's Musical Dynasphere - ANE, 1997 workshop
Keely Musical Dynasphere, IANS-1996
Keely's Musical Dynasphere
Part 19 - Musical Dynasphere - Historical
Roots of the Vibratory Etheric Tree - Keely's Musical Dynasphere
Resonation
REVOLVING SPHERE ROTATED BY VIBRATIONS
Sonication
Spirit Messages from John Keely, Atlin and Others as told to the Musical Dynasphere Project Team
Sympathetic Vibratory Physics - The Basic Principles
Symael
The Physics of Love 2.0
Universal Laws Revealed: Keely's Secrets
