A series of overtones that are harmonics of the fundamental pitch.
A series of overtones that are harmonics (ratios with common divisor or multiples of the divisor) with/of the fundamental pitch.
Law of Harmonic Pitch
"Any aggregate in a state of vibration develops in addition to its fundamental pitch a series of vibration in symmetrical sub-multiple portions of itself, bearing ratios of one, two, three or more times its fundamental pitch." [Keely, pre 1894]
Law of Harmonic Vibrations
"All coherent aggregates are perpetually vibrating at a period-frequency corresponding to some harmonic ratio of the fundamental pitch of the vibrating body; this pitch is a multiple of the pitch of the atomole." [Keely, pre1894]
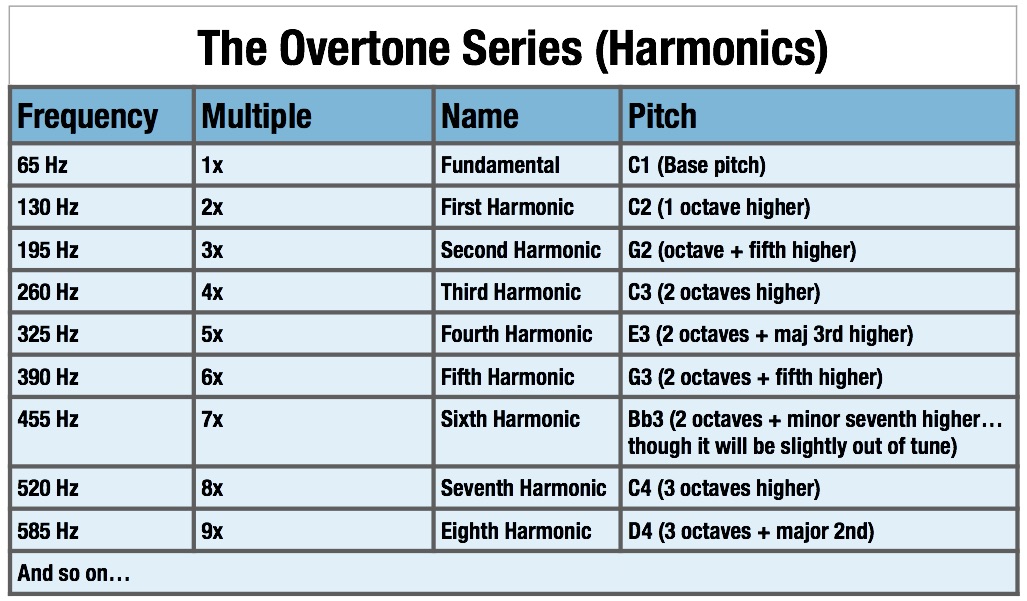
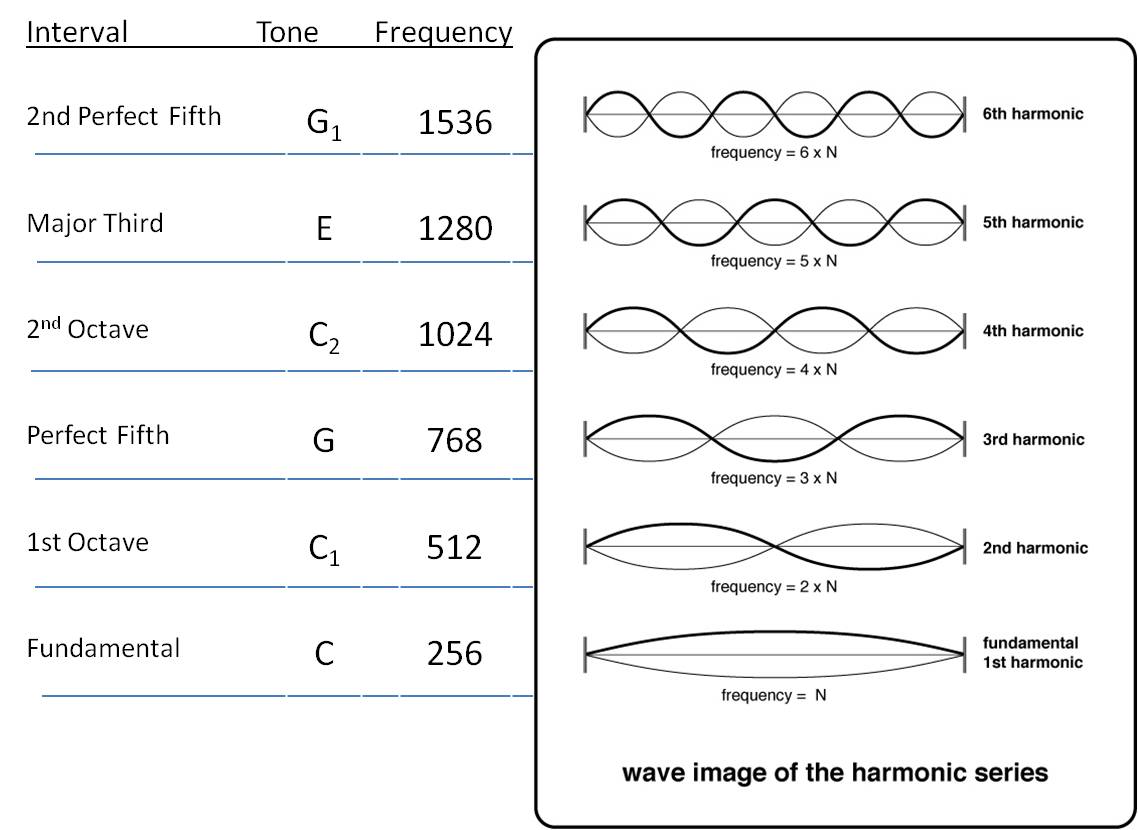
See Overtone Series
The harmonic series subdivides to create new tones between existing notes, and it does so in a very orderly manner (always at the center or mese of the interval). This is one reason why music theory overlaps monetary theory: if you create money based on a previous supply of "notes," as is done in the harmonic series, you prevent the unchecked expansion of the octave / debt economy. The octave is a beautiful thing, but it's firmly matter-based in the power of two and locked oscillation. The subdividing mese is a property of the power of three and breaks the locked oscillation allowing for flow. Until we understand this economically, we're easily manipulated by the debt-based economy in which we participate. [Stephanie McPeak Petersen]
Leonard Bernstein, in his famous Harvard speech, [The Unanswered Question 1973] truly explained why and how. Through his explanation of the harmonic series, he demonstrated the scientific basis of music theory. However, he also noted something profound: "What we calculate and explain or try to explain through music theory of Pythagoras, only appreciators of Indian music can feel it, they can demonstrate any mood through their scales, which they call Raaga. And a Raaga is not just a scale; it's something more. If you can't appreciate or feel it, it will put you to sleep in a few minutes."
See Also
1.23 - Power of Harmonics through Summation Tones
14.13 - Full Harmonic Chord
8.17 - Law of Harmonic Vibrations
8.22 - Law of Harmonic Pitch
9.23 - Circular Harmonic Orbit
9.24 - Elliptical Enharmonic Orbit
9.8 - Spontaneous Creation of Harmonic Series
9.9 - Sympathy or Harmony Between Harmonics or Overtones
Degree of Harmonicity
diatonic and enharmonic ring
diatonic enharmonic
Electromotive Series
Eleventh Harmonic
enharmonic scale
enharmonic sixths
enharmonic thirds
Enharmonic
Fibonacci Series
Figure 9.10 - Phases of a Wave as series of Expansions and Contractions
Figure 9.5 - Phases of a Wave as series of Expansions and Contractions
Full Harmonic Chord
harmonic combination
harmonic note
harmonic third
Harmonic Thirds
harmonic undulatory
Harmonic
harmonical parallel
harmonical ratio
harmonical triad
harmonics
Helmholtz Subharmonic Series
Keynote
Law of Harmonic Pitch
Law of Harmonic Vibrations
Master Tone
master tones
mathematical series of notes
Mid-tone
octave tones
Overtone Position
Overtone series
Power of Beat Harmonics
progression of harmonics
Ramsay - Ramsay's Extension of the Harmonics to Six Octaves
scale of Harmonics
second atomic harmonic
series of numbers
series of points in space which form a shaft
series of twelve
series
superharmonic
Table of Plate Harmonics and Intervals
three series
transuranium series
Triboelectric series
Vibrating Rod Harmonics
