Sympathetic Vibratory Physics

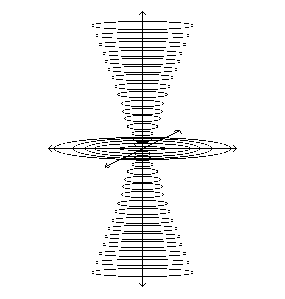
Vortex and Gyroscopic Motion on One Plane (left) then on three, forming Sphere.

The NEUTRAL CENTER is the infinite point in Space where these three modes meet.
Vortex pattern shows: Entropic, Syntropic and NEUTRAL modes.
Syntropic CENTERS are dynamic Etheric vacuous centers.
Entropic PERIPHERY is radiating violent motion.
The Entropic and Syntropic phases balance each other out (void). When predominance be given to the Syntropic the vortex will become tighter and more powerful. If predominance be given to the Entropic the vortex will increase in diameter and dissipate energy.

(click to enlarge)

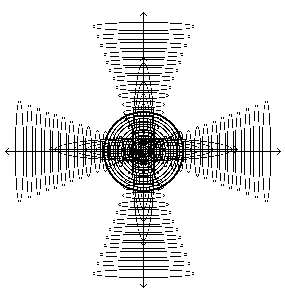
Figure 5.4 - Vortex and Gyroscopic Motion on One Plane (left) then on three, forming Sphere.

Alex Isakov
If a gyro rotating around one axis per cycle resists changing the position of the rotational axis and has two degrees of freedom in a holonomic mechanical system, then a gyro rotating around three axes per cycle resists changing the position around and along three axes per cycle and has 6 degrees of freedom - Gyro_6DoF. Such three-dimensional rotation of the rotor in the vacuumized stator cavity automatically leads to coherent oscillations of the points (mass elements) of the rotor.
Naturally, as in any known mechanical Gyro_2DoF and Gyro_3DoF gyroscope, the Gyro_6DoF rotor must resist the forces trying to change the positions of the rotation axes.
This means that Gyro_6DoF resists changing not only the angular orientation around each of the axes but also the motion along each of them. Each of the six directions of motion (three rotational and three rotational motions) is described separately, and six-coordinate parameters are required to fully describe the state of the gyroscope. Thus, the inertial mass of the rotor acquires the equivalent of an additional three-dimensional inertial mass depending on the rotational velocity of the spherical rotor Gyro_6DoF.
In a system like Gyro_6DoF, in which the rotor rotates about three different axes per cycle and resists changing position with respect to each of these axes, the inertial mass can depend on the rotor rotation speed. This means that the mass of the gyroscope can vary with its state of rotation and angular velocity. We will refer to this effect as "additional mass".
If the additional mass, according to Mach's principle, interacts with the mass of distant stars, then taking into account the proved anisotropy of the Universe at change of two or three axes of rotation of the rotor Gyro_6DoF to the center of mass of the rotor should be applied unidirectional and, what is very important, long-range inertial force, which can prove or disprove in experiment Mach's principle and allows to create devices to counteract gravitation (in full accordance with another proved principle - Einstein's equivalence principle).
Mach's principle states that inertial mass interacts with the mass of other objects in the Universe.
The anisotropy of the Universe implies that the physical properties of space can change depending on direction. If a unidirectional inertial force acts on the Gyro_6DoF rotor when two of the rotor's three axes of rotation are changed, this may be a consequence of the anisotropy of space reacting for matter in a coherent state.
Such experiments, if designed and performed, could have significant implications for our understanding of the fundamental laws of physics and the structure of the universe.
If the universal long-range force of inertia at ordinary rotational speeds of the Gyro_6DoF rotor (10000 cycles per minute) obeys Newton's second law, then, consequently, it acquires significant values and can reach units and even tens and hundreds of Newtons. [Alex Isakov]

Bridging Science and Spirituality

Search

Figure 5.4 - Vortex and Gyroscopic Motion on One Plane then on three forming Sphere