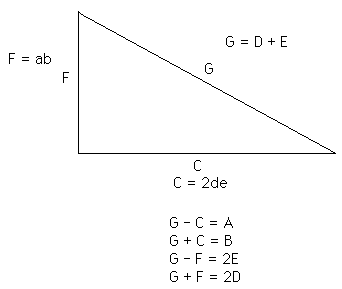Ben Iverson originated Quantum Arithmetic. During the 14 years he and I worked closely together I developed a number of new identities, procedures, rules and methods as additions and extensions to Ben's work. For instance this entire page was developed as I struggled to decipher his work and put it into a form that would be easily understandable to others. By illustrating each and every entity, point and law the whole thing began taking on clarity. Many new relations started showing up and new additions and extensions became obvious. When Ben said there was no way to define a circle with Quantum Arithmetic I developed three different ways to do this. These are contained herein. Ben often said the future of Quantum Arithmetic was in the 3-D world which he claimed he was not able to develop. I began the process as you can see on the Quaternion page because of the circles development and adding in the triple axis configurations of all vibrations. I also developed and added all the musical enhancements and calculations which are but simplistic attempts where I know many more years of work are needed.
This is only the beginning of where Quantum Arithmetic will eventually take us. I believe many new changes and modifications will be needed but the basic material appear to be good and solid. I feel certain as did Ben Quantum Arithmetic will serve best when used in a 3-D or even 4-D manners. For instance how can we extrapolate musical arrangements of the tones in sound into a sound field calculated using calculus with its squareness and imprecision? It cant be done with accuracy. One needs to use whole numbers to describe a whole number phenomena which sound is. Circles and areas will be the tools as opposed to linear quantities. Quantum Arithmetic appears to be the only method available and flexible enough to address this issue.
Also I wish to point out I do not believe Quantum Arithmetic (all by itself) will be the foundation math of sympathetic vibratory physics. There are elements in this math that will and do apply however. In the end I think we will have a system using parts from many different modes of arithmetic, music, mathematics, cycles, geometry and others. Dale Pond
In conventional math there have been four laws established along the order of logic and such things as Comutative association. The LAWS continue on into Quantum Arithmetic. There are quite a few basic laws and they expand into a whole field of logic in combinations of these laws. So let me get started.
1) Every Quantum Number consists of not less than three and not more than seven prime numbers, which also includes their powers. Only the first Quantum Number contains only two roots in 2x3=6 which is considered as the "ONE" of Quantum Arithmetic.
2) Every Quantum Number, in 2-dimensional math, must contain the prime number "2, and "3" or their powers. That means that only one number out of six cardinal numbers can qualify as a Quantum Number.
3) Once a Quantum Number is so identified by the two preceeding laws, it can be divided into its prime factors and their powers. These prime factors, and their products can then be so divided into four groups such the first group added to the second group will equal the third group, and the second group added to the third group will equal the third group, as the working roots, (b, e, d, & a), of a given Quantum Number. (Described beginning with Law #7) An extension of this Law says that this four number group can be formed in one way and one way only, but this portion of Law has not been proven. No standard method has yet been found to form this latter four-number group of roots from the factors. It can be done by "Quantizing" (See the last paragraph and Law #14).
4) Not an established Law for third-dimensional Quantum Arithmetic, but it is anticipated that a 3-diminsional Quantum Arithmetic,(QA), will include the number "5" also being required in addition to the "2" and "3". The smallest third-dimensional Quantum Number will be, 2x3x5=30 and only one integer in 30 will be a third-dimensonal Quantum Number
5) When a number is to be checked for factorability: (a) If it is an even number is divisible by "2"; (b) If the sum of the values of the digits is divisible by "3" then the number is divisible by "3"; (c) If the number (in the decinary notation), ends with a "0" or a "5", the number is divisible by "5".
6) The system of numbers is divided into four groups of parity. This is an extension, of "odd/even" from common math. When a number is divided by "4" it can have a remainder of 1 (or 5), 2, 3, or 0. They run in that cyclical order through the whole system of numbers. They are called "5-par, 2-par, 3-par & 4-par" respectively. (Euclid describes them as "even-odd, odd-odd, even-even and odd-even.". They each have distinctive characteristics, and form their own rules of parity, for addition, subtraction, multiplication, and powers, which rules will not be given here, at this time.
7) Every Quantum Number can be represented as the product of four roots. These roots will be displayed in Fibonacci fashion, (The sum of the first plus the second equals the third; and the sum of the second plus the third equals the fourth), and they will each be prime to the other three.
8) The first set of roots is 1, 1, 2, 3 and represents the "ONE". It will divide into roots of all other Quantum Numbers, and sets the stage for Quantum Creation.
9) Each set of Roots is unique. At least one will be prime in itself. The others may be products of two to four prime factors.
10) Roots are divided into two sets, separating the "male" from the female. The male roots will begin and end with odd numbers with one even number, and one odd number as intermediates. and may be considered to represent the x and y chromosome.
The female roots will begin and end with even numbers one of which is 2-par and the other 4-par, in either order. The two intermediate numbers will be odd. In this one case the "4" is considered to be prime to "2", and the "2" and "4" may be considered to represent the two x choromosomes.
11) The first female set of roots is 2, 1, 3, 4, and represents the female side of the "ONE" and the female side of Quantum Creation. In this case the "2" and the "4"(being a power of 2), can both appear in a set of Quantum Roots. In other higher cases the power of a prime represents but displaces its root prime. So a female Quantum number must contain an "8" and a "3" for the smallest Quantum Number of 24.
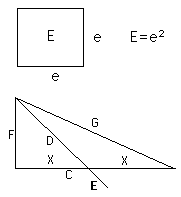
12) (a) Twice the product of the two intermediate roots will form the base of an unique Quantum right triangle.
(b) The sum of the squares of these two intermediate roots will form the diagonal of the same unique triangle.
(c) The product of the first and fourth Root will form the altitude of the same unique triangle.
(d) Twice the square of the intermediate will be the sum of the altitude and the diagonal of this unique triangle.
(e) Twice the sum of the square of the first and fourth roots will equal the difference between the diagonal and the altitude of this unique triangle.
(f) The square of the third root will be the mean of the altitude and the hypotenuse, of this same unique triangle.
13) Conversely:
(a) The difference between the base and hypotenuse of the triangle is
equal to the square of the first Root.(b)
(b) The sum of the base and the hypotenuse of the triangle is equal to
the square of the fourth Root.(a)
(c) Half the difference between the altitude and the hyotenuse of the
triangle equal to the square of the second Root.(e)
(d) Half the suj of the altitude and the hypotenuse of the triangle is
equal to the square of the third Root.(d)
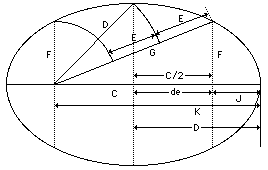
14) Every prime right triangle also represents the measurements within an unique ellipse.
15) The four Roots are represented along the major diameter of the ellipse:
(a) The first Root, (b), is represented in the perigee
(b) The second Root, (e), is represented as the half distance betwen foci.
(c) The third Root, (d) is represented in the semi-major diameter by the apogee.
(d) The fourth root,(a), is represented in the apogee.
16) In actual measurements in constructing an ellipse:
(a) The square of the third root,(d), is the semi-major diameter.
(b) The product of the first root, and the square root of the semi major-diameter, is equal to the actual measurement of the perigee.
(c) The product of the second root, and the square root of the semi-major diameter is equal to the half distance between foci.
(d) The product of the fourth root, and the square root of the semi-major diameter is equal to the actual measurement of the apogee.
(e) The product of the first root and the fourth root is the measurement of the semi-latera-recta
(f) The square of the third root is equal to the diagonal measurement from either focus to the midpoint of the locus of the ellipse.
(g) The sum of the squares of the two intermediate roots is equal to the diagonal measurement from a focus to the end of the opposite latus rectum.
END
This does not complete the present Laws by any means, but to give more at this time will overload the system, if it has not already.
The analysis of the major diameter of the ellipse in relation to its roots makes it possible to "Quantize" any valid Quantum number into its four roots. It will also "Quantize" any integer or non-integer and develop new unit-of-measure in which all measurements are in integers and integer relationships.
It is recommended that the reader concentrate on the first 11 Laws and commit them to memory and use before seriously beginning on the twelfth Law on.
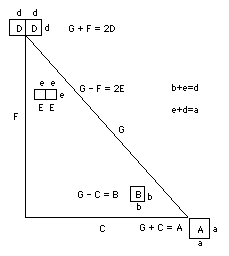
The hypotenuse added to the altitude equals the area of 2D. i.e., G + F = 2D.
The hypotenuse minus the altitude equals the area of 2E. i.e., G - F = 2E.
The hypotenuse added to the base equals the area of B. i.e., G - C = B.
The sides of these squares are d, e, a, and b, respectively.
They are in the format: b, e, d, a, in which b+e=d and e+d=a, as per Fibonacci, but he did not know this.C = (a2 - h2)/2
C = 2de
The value of C is the base or foundation number in every case.
C is the base in the triangle, and it is the distance between foci of the ellipse.
C is always an even number.
C is a 4-par number.
In the ellipse C maintains the orientation of the ellipse, and has a great deal to do with proportion.
C provides the baseline from which all of the other identities work.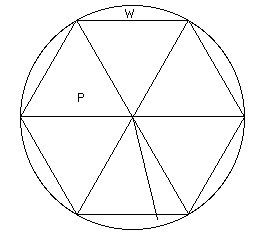
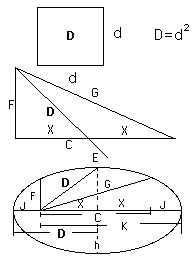
D = d2
D = (a2 + 2ab + b2)/4
The value of D is the next most important after C.
D is the mediator, being midway between F and G, and midway between J and K in the ellipse.
D plays two separate parts within every ellipse.
D is the semi-major diameter of the ellipse.
On the other hand, the value of D, is the distance from either focus to the midpoint on the rim of the ellipse. In this latter position, it also sets the value of the semi-minor diameter.No square number may be 2-par or 3-par.
Every 3-par number is the product of a 3-par and a 5-par number, or as the product of an odd number of 3-par products.
A 2-par integer is, "2", or a product of 2 and any odd integer. The odd number may be either 3-par or 5-par.
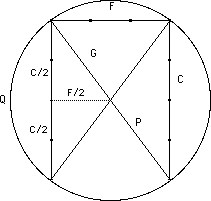
PAR NUMBER: [Quantum Arithmetic] A classification of numbers similar to mode 4 numbers with slight changes to comply with the requirements of Quantum Arithmetic. They are 2-par, 3-par, 4-par, and 5-par being respectively 4n-2, 4n-1, 4n, and 4n+1. The value of n is an integer but the integer value is never assigned. These are the four types of numbers described by Euclid as even-odd, odd-odd, even-even, and odd-even, with a main emphasis on excess and deficiency rather than on residue as applies to contemporary mathematics.The "doubling" of the roots is not a true doubling in the mathematical sense, but this doubling does "double" the value of all the other identities within the ellipse. Thus, the doubling of 1, 1, 2, 3 will give us 2, 1, 3, 4, but these two combinations are the roots of the 3, 4, 5, triangle and of the 6, 8, 10 triangle, which is a double of the first. The measurements of J, C/2, D, and K, along the major diameter of the same ellipse will be 2, 2, 4, 6 for the first roots and will be 6, 3, 9,12 for the second. This not a true doubling. The doubling occurs only in the triangle. A true doubling of the major diameter could not be because this ellipse is much more elliptical, but the triangle is truly doubled in its dimensions and quadrupled in its area. Along with that it is turned by ninety degrees in itself and within the ellipse which it represents. (see ROTATION herein for more information)
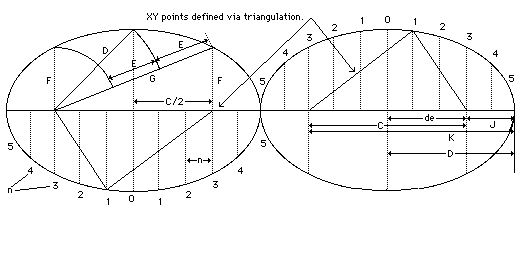
n has a linear value of d/e which is a prime fraction. x = nd/e. The quaternion points on the locus of the ellipse are integer radial values from both foci. See next card for more details.
The XY points of "1" alongthe perimeter are determined by triangulation from the Base C and Height F.

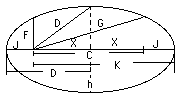
Elliptical functions are represented by J, F, D, G & K.
See also Quantum ellipses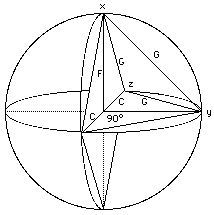
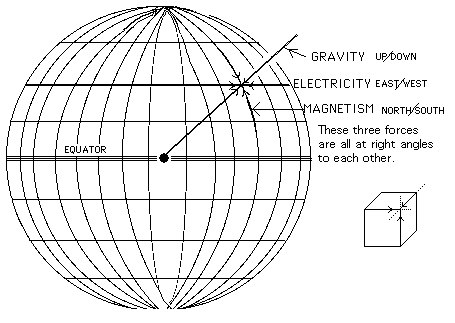
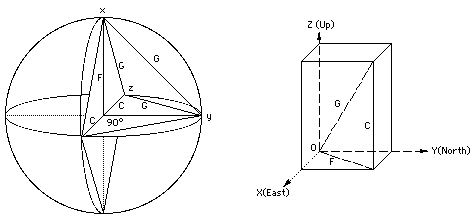
In an Equalized Sphere all vectors are equated, balanced or harmonized as 1 triune unit.
Confluence of C & G or F & G coincide with curve. In this case (of a sphere) F = C.
All CFG triangles depart from the center at 90°. This is an important point.
All CFG triangles are equal when in a sphere.
There are 12 equal CFG triangles in a sphere.
There are 4 per polarity or triplet
There are 24 equal CFG triangles in an ellipse.
There are 4 per polarity or triplet
There are 12 per Foci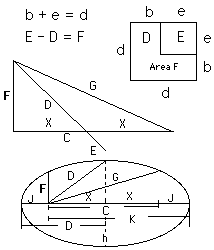
F = ab
F = d2 - e2
The number values which can be used for F are never prime numbers because F = ab and a and b are prime to each other. (except in the female set where one factor of , a or b, is 2-par and the other is 4-par.)
The value of F will be coprime to C, D, E, G, H, I.
F is also the height of the Prime Pythagorean Triangle.
F is of the odd parity.
Any and every odd integer can be a value for F, so long as that odd integer is the product of two odd numbers.
F can be either 3-par or 5-par.
(There is an exception in the female set where it is always the double of the base of the triangle of which the female set is the double. F represents the height of the triangle, but the triangle has been rotated 90°. In this set, F will always be an 8n integer. The base of this female triangle is a 2-par integer.)
The shape requirements for F are the most complex of any identity.
The number used for F must be a rectangle with dimensions a and b. F = ab.
The number used for F must also be able to form a gnomon which is shaped when F + E = D.
The outside length of the gnomon of F, will be d. The inside length of the legs will be e, the width of the legs will be b. b + e = d.
The values of F and G work together. They always stay equidistant from D, in value.
F and G begin at opposite ends of the orienting base, C.
In the ellipse they both start at the foci which are at the ends of C, giving them a stable base to work from.
With give and take of integers, between F and G, they sweep out the rim of an ellipse, always maintaining the value of D midway between them, as their mean.
The maximum values as they travel around the ellipse is K.
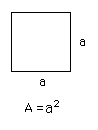
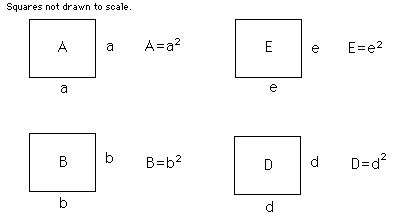
The minimum value of F and G is J.1) b = root b2 = B
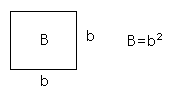
2) e = root e2 = E
3) d = b+e d2 = D
4) a = e+d a2 = A
5) B = b*b = Area of b
6) E = e*e = Vector extension of right triangle E = e*e = Area of e2
7) D = d*d = Vector on right triangle D = d*d = Half width of ellipse D = d*d = Locus to apex on ellipse D = d*d = Area of d2
8) A = a*a = Area of a2
9) X = e*d = Half length of right triangle X = C/2 = Quarter width of ellipse
10) C = e*d*2 = Length of right triangle C = e*d*2 = Loci distance on ellipse
11) F = b*a = Height of right triangle
12) G = D+E = Hypotenuse of right triangle G = dd+ee = Locus to semi-apex on ellipse
13) L = C*F/12
14) H = C+F
15) I = C-F (result must be a positive number)
16) J = d*b = Distance of loci to outer width of ellipse
17) K = d*a = Furthest loci to outer width of ellipse
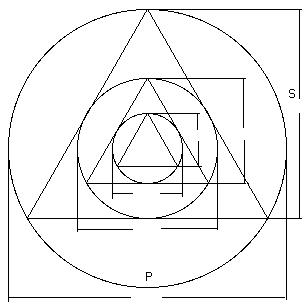
18) W = d(e+a) = Side of equilateral triangle W = K+C/2 W = de+da W = X+K
19) Y = A-D
20) Z = E+K Z = ee+K Z = e2 + (a*d)
21) h = d(a*b) = Half height of ellipse
22) P = 2*W = Diameter of circle
23) Q = P = Circumference of circle
24) R = W2 = Area of circle
25) S = d*X = Height of equilateral triangle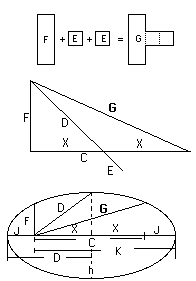
G = C + B
G = F + 2E
G = D + E
G = (a2 + b2)/2
G = d2 + e2
G (the hypotenuse) must always be a 5-par number.
G is greater than F by 2E.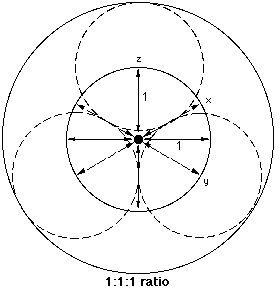
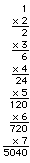
1 x 2 x 3 x 4 x 5 x 6 x 7 = 5040
71 x 71 = 5041
7 x 8 x 9 x 10 = 5040
Pythagoras said: "The numbers stop at 10." [as in the column sum of multiples.]H = (a2 + 2ab - b2)/2
H = d2 + 2de - e2
The prime numbers are symmetrical. All odd composite numbers are covered by one cycle or another.
They are: 15, 21, 33, 35, 39, 45, 51, 55 and 57.I = (a2 - 2ab - b2)/2
I = e2 + 2de - d2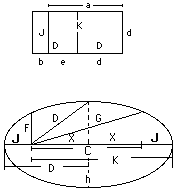
J = b*d.
J = (d2 - de)
J = D - de
J = (b2 + ab)/2
J only appears in the ellipse and not in the triangle.
J is never prime.
J shares common factors with B, C, D, F & L.
The value for J has no specific parity requirement.
J may have any parity which is controlled by the factors b and d.
The shape of J is always a rectangle, paired with K and having one dimension, d, in common.
The J rectangle also has b for its other dimension.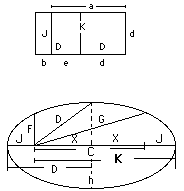
K = a*d.
K = a2 + ab)/2
K = (d2 + de)
K appears in the ellipse and not in the triangle.
K is never prime.
K shares common factors with A, C, D, F & L.
The value for K has no specific parity requirements.
K may have any parity, which is controlled by the factors a and d.
K is always a rectangle paired with J in such a fashion as to share one dimension, d.
The K rectangle will have a short dimension of d; and a long dimension of a.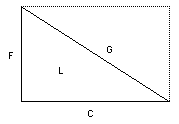
L = (a3b - ab3)/6
L = (d3e - de3)/6
L = FC/2
L is the AREA of the Prime Pythagorean Triangle.
L is never prime because it will have the factors b, e, d, & a.
L has no strict parity requirements.
The geometric shape of L is more complex than any of the other identities.
In some ways L may be considered as a 4-dimensional solid.The Line has length and breadth. Some may argue it has any breadth but for it to be a line of any magnitude whatsoever that magnitude is some quantity and the least quantity possible is always 1.
For it to be a Line (which is more than a point) its length must be greater than 1 (its breadth) and the least quantity greater than 1 can only be 2.The Point has no dimension but it does have quantity.
Therefore its mathematical description means:
a quantity X to the zeroth dimension = 1.
The Point is dimensionless yet it has quantity and the least real quantity is always and can only be 1.
see QUATERNION in this stack for more discussion concerning dimensions.1. All integers are divided into two classes: odd and even.
2. All even integers are divided into two classes: 2-par, (4n-2) and 4-par, (4n) integers.
3. All odd integers are divided into two classes: 3-par (4n-1), and 5-par, (4n+1).
4. Only 4-par and 5-par numbers may be squares of integers. 2-par and 3-par integers may not, but all four may be rectangles.
5. Both odd and even integers further divides each of its classes into pairs of classes on a binary basis, around 8, 16, 32, 64, etc.
6. The base, C, of a triangle, and the line joining foci of an ellipse must be a 4-par integer. (Doubling changes this to 2-par.) This 4-par integer is the foundation number in every mathematical case in Quantum Arithmetic around which all the integers of a detail will build. And in the vein of Pseudaria, this 4-par integer maintains its group of integers in a strict orientation and polarity when they build upon it. This base is always divisible by four in its prime useages, (but divisible by 2 after a doubling takes place.)
7. The altitude F, of a triangle, is always divisible by three, or by some higher odd integer. When not divisible by three, then the base is divisible by three as well as by four. (i.e., divisible by 12). The altitude of a triangle will form a gnomon which is the difference of two squares, and a rectangle, in as many as it has divisors less than the square root of the integer representing it.
8. The hypotenuse, G, of a triangle, must be divisible by 5, or be some higher integer which is 5-par. It cannot be divisible by 3 or 4. If G is not divisible by 5 then the altitude, F, must be divisible by 5. If the hypotenuse or the altitude are not divisible by 5 then the base must be so divisible in addition to its other duties. The hypotenuse must be the sum of two squares, (D and E), and must be the mean of two squares, (B and A).
9. The mean of the altitude, F, and the hypotenuse, G, must be a square number, D, and must differ from them by another square, E, which is of an opposite parity. Of these two squares, one must be 4-par, and the other must be 5-par.
10. The value of the hypotenuse, G, as the mean of two sqares, A and B, will differ from them by a 4-par number, C, and both squares must be odd and 5-par integers.
11. Every operation with a group of connected integers will have a system of four roots, b, e, d, and a, underlying the operation. One of these roots, d or e, must be even, and the other three must be odd. (Doubling changes the rule.)
12. One of the four roots must be divisible by three.
13. One of the four roots must be divisible by five, or the sum of the squares of the two center ones, d and e, must be divisble by 5. (vis. must be 5-pent or 5n in character.)Q = Circle Circumference
There are four presently known ways to quantize an ellipse. Regardless of which measurements are given to dictate the way for quantizing the ellipse, one must eventually reduce this to finding the value of D or d2. Once the value of D is found then one other root must be located. So, some pairs of given measurements result in a fairly simple solution, but other pairs make the solution complex.
1) If the values of F and G are given, the method is quite simple because D is the mean of F and G and E is the variation from the mean. In this case (G + F)/2 = D and (G - F)/2 = E.
2) If the values of C and G are given, one can complete the triangle and use the above method, or one can use the feature that G is the mean of two squares, A and B, and C is the variation from the mean. In this case G + C = A and G - C = B which are a2 and b2. The other two roots, d, and e, are the mean, and the variation from the mean of a and b.
3) A third method will result when C and F are given. Again, one can complete the triangle and use the first method. Or one can depend upon the feature that G2 is the mean of I2 and H2, which are (C - F)2 and (C + F)2 respectively. This still does not resolve any of the roots and one must revert to either of the first two methods.
4) The fourth method involves having any two of the measurements along the major diameter, (Or line of apsides). This method is the most acceptable and accessible because these can be the most accurate and all four measurements can be easily determined. The four measurements then contain all four roots of the ellipse. They are J = bd, C/2 = ed, D = d2, and K = ad. Of these, D is the square of the root d. Then dividing any of the other measurements by this root will produce their other root. This method is used almost exclusively in this text, and is the basis for the computer program given elsewhere.Music Intervals of a Pythagorean Triangle.
| identities ratio | ||
| Unison | 1:1 | |
| Octave | 2:1 | |
| Perfect Fifth | 3:2 | |
| Major Third | 5:4 | G:F |
| Perfect Fourth | 4:3 | F:C |
| Major Tenth | 5:2 | |
| Perfect Twelfth | 3:1 | C:L |
| Major Sixth | 5:3 | G:C |
| Double Octave | 4:1 | F:L |
Space is divided into at least 12 dimensions. There are the three conventional dimensions, and each of these is divided into four sub-dimensions.
The first and basic sub-dimension is the quaternion, the unit of which has a diameter of one unit, or a cube which is one unit on a side. This unit is so miniscule that we may consider it dimensionless. We take this unit to be on the order of 10-14 millimeter. The quaternion is the equivalent of a point in space, in Quantum Arithmetic.
The second sub-dimension is the product of two quaternions, and is considered on the same basis as a line. It is used here as a root, and has length but its width and thickness is the unit quaternion. The root is the equivalent of a point (qv) in space in conventional mathematics. It is represented by b, e, d, or a.
The third sub-dimension is the product of two roots or the product of four quaternions. It is an area in Quantum Arithmetic, but considered as a line in conventional methematics. It is represented by any of the capitalized identities, A through K. This dimension has length and width but its thickness is the unit quaternion.
The fourth dimension in Quantum Arithmetic is the product of two of the third-dimensions; of four of the roots; or of eight of the quaternions. It will have measurable length, width and thickness. It is represented in the capitalized identities by L, (L = beda/6), or by the squares of any of the other capitalized identities, (C2 + F2 = G2). In Quantum Arithmetic this dimension is a solid. In conventional methmatics it is undefined. (The area of an ellipse is the product of pi and three roots, d3, and two quaternions, a, and b, in square units. For the same measurement in circular units it is : Area = d3ab).
This last dimension has had little discussion in this text, partly to avoid going into the higher dimensions, and partly because this higher dimension and its relationship to conventional dimensions, has not been investigated. When these lower dimensions are more fully understood then the upper dimensions will fall into place. It is anticipated that a 5-way division is involved, and that the conventional 3-dimensions, the 4-dimensions of Quantum Arithmetic, and the unexplored 5-dimension system will, working through Synchronous Harmonics, make a 60-way division of space, hence the viability of the sexigesimal system of numerical notation.
The system of integers forms an associated symmetry around a square of an integer, D. Each pair of integers will have a complimentary system of characteristics for par-value, primeness/factorability, and shape. The arrangement goes into greater detail as more subsidiary integers are added to the framework.
General: Although the ellipse is derived through porisms (qv), the aspects of the ellipse discussed here; the role of C in maintaining the orientation of the ellipse; the role of E as a mediator of the ellipse and the role of J, F, G, and K in the operational phases; are all in the field of Pseudaria. In retrospect, and particularly in the derivation of fractional equivalents, lead to a deeper meaning in that the ellipse may be only a frame of reference in which these are taken. This has all been done through constructive geometry because it would have been relatively impossible to approach and describe in an abstract sense. This four-way division of duties between C, D, E, and the operators, J, F, G, and K can be extended outside the realm of mathematics and into many other fields. Plato refers to these duties in Republic, but in a philosophical sense. Quantum Arithmetic leads almost naturally into the humanities and far beyond the limits of conventional mathematics.After using the Quantize program for a short time, one will notice that some of the roots have a series that begin and end with even numbers, and the two center ones, e and d, are odd. This points up something which was thought trivial about the Prime Pythagorean triangles, but appears to be quite important. These even valued roots inject a concept of "doubling" or the influence of "2". The ellipse which these roots project, is turned on end, that is, the ellipse is rotated through ninety degrees, when b > e, (vis; N > O), after doubling. (see DOUBLING)
The rotation of the ellipse is perhaps best demonstrated by reverting to the prime Pythagorean triangle from which the ellipse derives. In such a triangle, the sum and difference of the hypotenuse and altitude, G and F, is always a double square. At the same time the sum and difference of the hypotenuse and base, G, and C, are single squares. In the "doubling" process, the double of a single square is a double square, but the doubling of a double square is a single square. This, in effect, reverses the position of D and E, with A and B. Then such a triangle is considered to be rotated through ninety degrees.
But the "doubling" process is not particularly a mathematical doubling. In fact it has nothing to do with doubling. In this doubling process the ellipticity of the ellipse is actually drastically changed. All ellipses fall on one side or the other of the basic ellipse which begins with the roots, 1, 1, 2, 3, which are in turn, representative of the 3, 4, 5, Prime Pythagorean triangle. When an ellipse or triangle have roots which are near to this value the doubling process causes little change. One side will have ellipses slightly more circular. The other side of this median will have ellipses slightly more elongated.
If this "doubling" (see DOUBLING) concept has a reality and an application it would be in the case of the correlation between Earth orbit and the orbit of Halleys Comet. Note that the quantum numbers for them 1, 29, 30, 59, and 59, 1, 60, 61. This combination indicates that Halleys Comet has some special relationship with Earth. The "59" used as roots in both cases indicates a close synchronization between them, and the "1" in each case indicates a highly stabilized orbit, for each of them.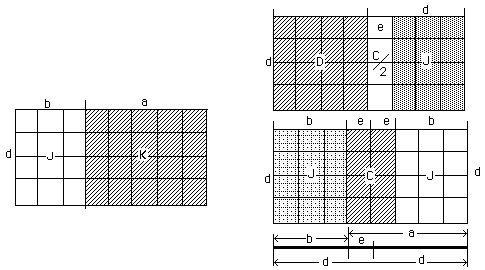
THE ONE is composed of two squares: One male, one female. They break into 3 rectangles, C, J & K, and into 3 more squares, A, B & E.
Capital letters are areas. Lower case are distances. b+e=d, e+d=a.
In this case b=3; e=1; d=4; a=5. There may be other coprime values.DP: This was a beginning effort to marry QA to SVP. I think it can only work via 3-D and 4-D projective geometry. Another connection is the two foci of an ellipse. See links below.
See Also
Apsidal
Arithmetic
cube-sphere - Cubing the Sphere
Cubing the Sphere
East-West spherical planes
Figure 9.7 - Two Centers Showing Complex Attraction Dynamics
Geometry
Iverson
Iverson's books on Quantum Arithmetic
Number
Prime Fraction Equivalent
Quadrature of the Circle
Quantization - Physics
Quantize to One
Quantize
Quantum Arithmetic
spherical coordinates
two centers
two controlling points of stillness
two dividing poles
two lights of the spectrum
two opposed electric forces
two points of stillness
two poles
two-way compression-expansion sequence
two-way divided effects of motion
two-way effect
two-way extension of a point in space
two-way motion
two-way opening and closing universe
two-way universe
What is Quantum Arithmetic?
12.38 - Orbital revolution
9.23 - Circular Harmonic Orbit
9.24 - Elliptical Enharmonic Orbit