Resonance, Co-vibration, or Sympathy of Tones.

Select two tuning-forks which are exactly in unison. Having taken one in each hand, strike that in the right hand pretty sharply and immediately hold it with its prongs parallel, and close to the prongs of the other, but without touching it. After the lapse of not less than one second, on damping the fork in the right hand, than in the left will be found to be giving out a feeble tone. To this phenomenon, the names of Resonance, Co-vibration, and Sympathy of tones have been given, the first being the one most commonly used in English works. The explanation of this effect will be better understood after a consideration of the following analogous experiment.

Let a heavy weight be suspended at the end of a long cord, and to it attach a fibre of silk or cotton. The weight being at rest, pull the fibre gently so as not to break it. The weight will thus be pulled forwards through an exceedingly small, perhaps imperceptible distance. Now relax the pull on the fibre, till the weight has swung through its origin position, and reached the limit of its backward movement. If another gentle pull be then given, the weight will swing forward a trifle further than at first. The weight then swings backwards as before, and again a properly timed pull will still further extend its excursion. By proceeding in this way, after a time the total effect of these accumulated impulses will have been sufficient to impart to the weight a considerable oscillation. On examination it will be found that this experiment is analogous to the last one. The regularly timed impulses in the second experiment, corespond to the regularly vibrating fork in the right hand; the weight to the fork in the left hand, and the fibre to the air between the forks. And here it must be observed that just as the forks execute their vibrations in equal times, whether their amplitudes be great or small, so the weight performs its swings (as long as they are not too violent) in equal times, whether their range be small or great. Again, the conditions of success are the same in both cases; for, in the first place, the impulses in the second experiment must be exactly timed, that is, they must be repeated at an interval of time which is identical with the time taken by the weight to perform a complete swing. In other words, the hand which pulls the fibre must move in perfect unison with the weight. If this were not so, the impulses would destroy one another's effects. Just so with the forks; they must be in the most rigorous unison, in order that the effects of the impulses may accumulate. Again, in each experiment a certain lapse of time is necessary to allow the effects of the successive impulses to accumulate.

The complete explanation of the experiment with the two tuning forks is as follows. Let the prong A of the fork in the right hand be supposed to be advancing in the direction of the non-vibrating fork B; the air between A and B will be compressed, and thus the pressure on this side of the prong B will be greater than that on the other; the latter prong will therefore move through an infinitesimal space away from A. Now suppose the prong A has reached its extreme position and is returning; then, as both forks execute their vibrations in exactly equal times, whether these be of large or small extent, it follows that B must be returning also; but as A moves through a greater space than B, the air between the two will become rarefied, and thus the pressure on this side of B will be less than that on the other; B will therefore receive another impulse, which will slightly increase its amplitude. On its return, it will receive another slight impulse, and thus, by these minute successive additions, the amplitude is soon sufficiently increased to produce an audible sound.

In the preceding experiment, the exciting fork communicates a small portion of its motion to the air between the forks, and then this latter gives up part of its motion to the other fork. Now, as the density or weight of air is so exceedingly small in comparison with that of the steel fork, the amplitude of the vibrations thus set up in the latter must necessarily be always very small, that is, its sound will be very faint. By using a medium of greater elasticity, the sound may be obtained of sufficient intensity to be heard by several persons at once. Thus, let one fork be struck sharply, and the end be immediately applied to a sounding board, on which the end of the non-vibrating fork is already resting; after the lapse of a second or so, the latter will be heard giving forth a sound of considerable intensity, the motion in this case having been transmitted through the board.

The following experiments illustrate the phenomenon of resonance or co-vibration in the case of stretched strings. Press down the loud pedal of a pianoforte, so as to raise the dampers from the strings. Each sound on the pianoforte is generally produced by the vibration of two or three wires tuned in unison. Set one of these vibrating, by plucking it with the finger. After the lapse of a second or so, damp it, and the other wire will be heard vibrating. Again, having raised the dampers of a pianoforte, sing loudly any note of the piano, near and towards the sound board. On ceasing, the piano will be heard sending back the sound sung into it. The full meaning of this experiment will be explained hereafter.

The resonance of strings may be visibly demonstrated to an audience in the following manner. Tune two strings on the monochord or any sound board, in perfect unison, and upon one of them place a rider of thin cardboard or paper. On bowing the other string very gently, the rider will be violently agitated, and on increasing the force of the bowing, will be thrown off.

In these experiments the sound board plays an important, or rather an essential part. Thus, in the above experiment with the piano, the sound waves from the larynx of the singer strike the sound board of the piano, setting up vibrations in it, which are communicated through the bridges to the wires. It will be found that in these experiments with stretched strings, such perfection of unison as was necessary with the forks is not absolutely essential, and the reason is obvious; for in the first place, the medium by which the vibrations are communicated in the former, viz., the wood, is much more elastic than in the latter; and secondly, the light string or wire is much more easily set in vibration than the heavy steel of the fork. A smaller number of impulses is therefore sufficient to excite the string, and consequently such a rigorous unison is not absolutely essential. As we might expect, however, the more exact the unison, the louder is the sound produced.

In consequence of their small density, masses of enclosed air are very readly thrown into powerful co-vibration. Strike a C1 tuning fork, and hold the vibrating prongs over the end of an open tube, about l3 inches long and about an inch in diameter. The sound of the fork, which before was very faint, swells out with considerable intensity. The material of the tube is without influence on the result. A sheet of paper rolled up so as to form a tube answers very well. On experimenting with tubes of different lengths, it will be found that the sound of the C1 fork is most powerfully reinforced by a tube of a certain length, viz., about 13 inches. A slightly shorter or longer tube will resound to a smaller extent, but little resonance will be obtained, if it differs much from the length given. Before reading the following explanation of this phenomenon, the student should read over again the account given in Chapter II of the propagation of sound.

Let A B, fig. 32, represent the tube, with the vibrating tuning fork above it. As the lower prong of the latter descends, it will press upon the air particles beneath it, giving rise to a condensation, A C.

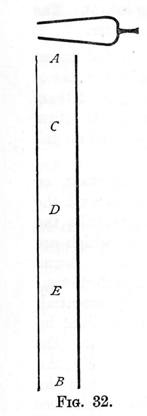
The particle in A C being thus crowded together, press upon those below, giving rise to a condensation C D; the particles in which, in their turn, press upon those beneath, thus transmitting the wave of condensation to D E. In this way, the condensation passes through the tube, and at length reaches the end, E B. The crowded particles in E B will now press outwards in all directions, and overshooting the mark, will leave the remainder farther apart than they originally were; that is, a rarefaction will be formed in E B. But as there is now less pressure in E B than in D E, the particles of air in the latter space will tend to move towards E B, and they themselves will be left wider apart than before; that is, the rarefaction will be transmitted from B E to E D, and in like manner will pass up the tube till it reaches A C. On arriving here, as the pressure in A C will be less than the pressure outside the tube, the air particles will crowd in from the exterior and give rise to a condensation. Thus, to recapitulate; the downward movement of the prong gives rise to a slight condensation in the tube below; this travels down the tube to B, where it is reflected as a pulse of rarefaction; this, rushing back, on reaching A is changed again to a pulse of condensation. Now if, while this has been going on, the fork has just made one complete vibration, the lower prong will now be coming down again as at first, and thus will cause an increase in the degree of condensation. The same cycle of change will take place as before, and will recur again and again, the degree of condensation and rarefaction, that is, the intensity of the sound, rapidly increasing to a maximum. To compare this with the experiment of the suspended weight:- the vibrations of the fork correspond to the properly timed impulses, and the air in the tube to the suspended body; and, just as in that experiment, the essential point was the proper timing of the impulses, so in this case the essential matter is, that the downward journey of the condensation, shall coincide with the downward movement of the prong. In order that this coincidence may occur each time, it is evident that the wave must travel down and up the tube in exactly the same time that the fork makes one vibration; that is, while the fork makes one vibration the sound must travel twice the length of the tube. Moreover, every vibration of the fork gives rise to one sound wave; therefore, in order that a tube open at both ends may give its maximum resonance when excited by a fork, it must be half as long as the sound wave originated by that fork.

It will be seen that a certain amount of resonance is obtained if the tube is twice this length; for in that case, every alternate descent of the prong will coincide with a condensation below, and each alternate ascent with a rarefaction; but such resonance will evidently be much feebler. For intermediate lengths, the fork will soon be in opposition to the pulses in the tube, and thus no resonance can result.

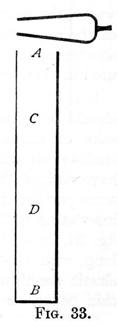
Tubes closed at one end are termed stopped tubes; with these the case is somewhat different. Let A B, fig. 33, represent a stopped tube, the lower prong of the tuning fork above, being about to descend towards it. As we have already seen, this gives rise to a condensation A C, which travels down to B D. The air particles in B D, having no way of escape, save backwards, press upon those in C D, and thus the condensation is reflected back to C D, and finally to A C. From here some of the condensed particles escape into the external air, leaving the remaining particles slightly wider apart; that is, a slight rarefaction is formed. If while this has been taking place, the prong has reached its lowest position and is just returning, this movement will have the effect of increasing the rarefaction. This latter will then be transmitted down the tube to B D. On reaching this, there will be less pressure in B D than in D C, and consequently the air particles in the latter will crowd into the former, causing a rarefaction in C D. In this way the rarefaction is transmitted back to A C. As the pressure of the external air will now be greater than that in A C, air particles from the former will crowd in, forming a condensation in A C. If at this moment, the prong is a second time beginning its descent, this condensation will be increased, and the same series of changes will take place as before. It is evident, therefore, that the sound wave must make two complete journeys up and down the tube, while the fork is executing one vibration; that is, in order that a stopped tube when excited by a fork, may give its maximum resonance, it must be 1/4 as long as the sound wave originated by that fork.

We have already seen, that the length of the sound wave produced by a sounding body, may be ascertained by dividing the velocity of sound by the vibration number of that body; consequently it is easy to calculate the length of tube, either open or stopped, which will resound to a note of given pitch. The rule evidently is: divide the velocity of sound by the vibration number of the note; half this quotient will give the length of the open pipe, and one fourth will give the length of the stopped one. It is necessary that the tube should be of moderate diameter, or the rule will not hold good, even aproximately.

The resonance of stopped tubes may easily be illustrated, by means of glass tubes, corked, or otherwise closed at one end. On holding a vibrating tuning fork over the open end of a sufficiently long tube, held with its mouth upwards, and slowly pouring in water, the sound will swell out when the vibrating column of air is of the requisite length, the water serving the purpose of gradually shortening the column. For small forks, test tubes, such as are used in chemical work, are very convenient.

It is by no means necessary that the resounding masses of air should be in the form of a cylinder; this shape was selected for the sake of simplicity in explanation. Almost any shaped mass of enclosed air will resound to some particular note. Everyone must have noticed, that the air in a gas globe, vase, &c., resounds, when some particular sound is loudly sung near it. The following is an interesting method of optically illustrating this phenomenon. A, fig. 34, is a cylinder 3 or 4 inches in diameter, and 5 or 6 inches long, with an open mouth, B. The other end is covered with an elastic membrane, D, such as sheet india-rubber slightly stretched thin paper, or membrane. At C is fastened a silk fibre, bearing a drop of sealing wax, hanging down like a pendulum against the membrane. If now anyone places himself in front of the aperture, and sings up and down the scale, on reaching some particular sound the pendulum will be violently agitated, showing that the membrane and the air within the bottle are vibrating in unison with that note.

Another simple experiment of the same kind can be performed with a common tumbler. Moisten a piece of thin paper with gum, and cover the mouth of the tumbler with it, keeping the paper on the stretch. When dry cut away a part of the paper as seen in fig. 35.

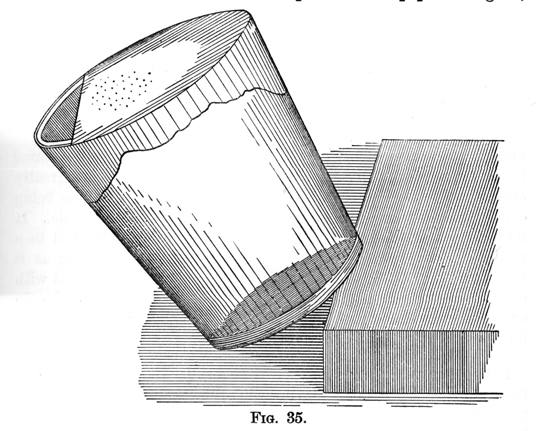
Put a few grains of sand, or any light substance on the cover, and then tilt up the glass, so that the sand will nearly but not quite, roll off. Having fixed the glass in this position, sing loudly up and down the scale. On reaching a certain note, the co-vibration of the air in the tumbler will set the paper and sand into violent vibration. By singing a sound of exactly the same pitch as that to which the air in the tumbler resounds, the sand may be moved when the singer is several yards away. See Volumetric Resonator

The phenomenon of resonance is taken advantage of, in the construction of resonating boxes. These are simply boxes (fig. 36), generally made of wood, with either one or two opposite ends open, and of such dimensions, that the enclosed mass of air will resound to the tuning fork to be attached to the box.

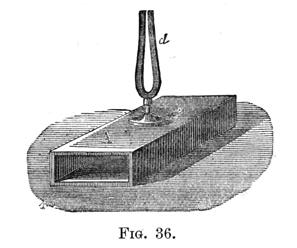
Such boxes greatly strengthen the sound of the fork, by resonance; the vibration being communicated, through the wood of the box, to the air inside. It may be remarked here, that the sound of a fork attached to a resonance box of proper dimensions, does not last so long as it would, if the fork were held in the hand and struck or bowed with equal force; for in the former case it has more work to do, in setting the wood and air in vibration, than in the latter, and therefore its energy is sooner exhausted.

For forks having the vibration numbers in the first column of the following table, boxes having the internal dimensions given in the 2nd, 3rd, and 4th columns are suitable. The dimensions of the first four are, for boxes open at one end only; those of the last four, for boxes open at both ends. The fork is screwed into the middle of the top of the box. The dimensions are in inches.

Vibration No.	Length.	Width.	Depth.
128	22.2	11.6	6.1
256	11.5	3.8	2
384	7.3	3.2	1.8
512	5.4	2.7	1.5
640	8.8	2.7	1.4
768	7.8	2.3	1.3
896	6.2	2.1	1.1
1024	5.5	1.9	1

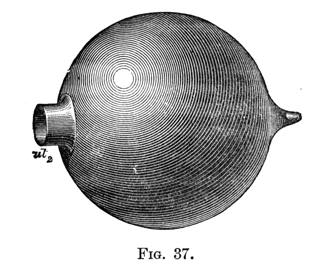
A Resonator is a vessel of varying shape and material, and of such dimensions, that the air contained in it resounds, when a note of a certain definite pitch is sounded near it. Resonators are most commonly constructed of glass, tin, brass, wood, or cardboard. The former most often met with are the cylindrical, spherical, and conical. There is to enable the ear to distinguish a sound of a certain pitch, fro m among a variety of simultaneous sounds, of different pitches. The only essential, therefore, in the construction of a resonator is, that the mass of air which it encloses shall resound to the note which it is intended to detect. The best form for a resonator designed for accurate scientific work is the spherical, as it then reinforces only the simple sound to which it is tuned. The spherical resonators employed by Helmholtz in his researches, were of glass, and had two openings as shown in fig. 37.