The Transmission of Sound
We have seen in the preceding chapter, that all sounds originate in the vibratory movements of bodies. This vibratory motion is capable of being communicated to, and transmitted by, almost all substances, to a greater or less extent. Wood, glass, water, brass, iron, and metals in general may be taken as examples of good conductors of sound. But the substance, which is the vast majority of cases transmits to our ears the vibratory motion, which gives rise to the sensation, sound, is the air.
A very little reflection is sufficient to show us that some medium is absolutely necessary for the transmission of sound; for inasmuch as sound is caused by vibratory motion, it is plain that this motion cannot pass through a vacuum.(1) This fact can, however, be easily proved experimentally. Under the receiver of an air-pump a bell is suspended. We shake the pump, and the bell may be heard ringing; for its vibrations are communicated by the air to the glass of the receiver, and by the latter to the outer air, and so to our ears. We now pump as much air as possible out of the receiver, and again ring the bell. It can still be heard faintly, for we cannot remove all the air. We now allow dry hydrogen to pass into the receiver, and on again ringing the bell, there is very little increase of sound, this gas being so very light-only about 1/14 as heavy as air. If we now exhaust the receiver, we shall be able still further to attenuate the atmosphere within it, and then, although we may violently shake the apparatus, no sound will be heard.
As the air is generally the medium, by means of which the vibratory motion reaches our ears, we shall now have to carefully study the manner in which this transmission takes place. When we stand on the sea shore, or better still, on a cliff near it, and watch the waves rolling in from afar, our first idea is, that the water is actually moving towards us, and it is difficult at the time to get rid of this notion. If, however, we examine a little more closely, we see that the boats and other objects floating about, do not travel forward with the wave, but simply rise and fall as it passes them. Hence we conclude that the water of which the wave is composed, is not moving towards us. What is it, then, that is being transmitted? What is it that is moving forwards? The up and down movement - the wave motion. Now the vibratory movements which give rise to sound are, as we shall presently see, transmitted through the air much in the same way; and therefore, although a sound wave is not exactly analogous to a water wave, yet a brief study of the latter will help us more easily to understand the former.
Let ADECB (figure 7) represent the section of a water wave, and the dotted line AEB the surface of still water. That part of the wave ADE above the dotted line, is termed the crest, and the part ECB below, the trough.
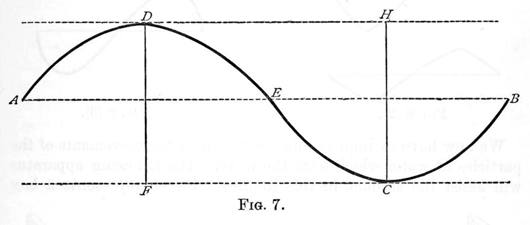
Through D and C, the highest and lowest points, draw DH and FC, parallel to AB, and from the same points draw DF and CH perpendicular to it. Then the distance AB is termed the length of the wave, DF or CH is its amplitude, and the outline ADECB is its form.
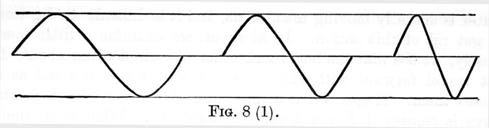
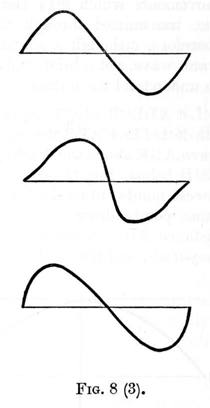
These three elements completely determine a wave, in the same way as the length, breadth and thickness of a rectangular block of wood, determine its size; and further, as any one of these three dimensions may vary independently of the other two, so any one of the three elements - length, amplitude, and form - may vary, the other two remaining constant. Thus in figure 8 (1),
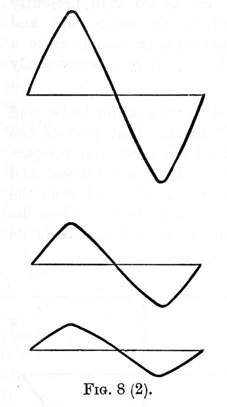
we have three waves of the same amplitude and form, but varying in length; in figure 8 (2) we have three waves of same length and form, but of different amplitudes; while in figure 8 (3), we have three waves of same length and amplitude, but of varying forms.
We now have to inquire into the nature of the movements of the particles of water which form the wave. The following apparatus will assist the student in this inquiry. Figure 9 represents a box about four feet long, four inches broad, and six inches deep, with either one or both the long sides of glass, and caulked with marine glue, so as to be water-tight.
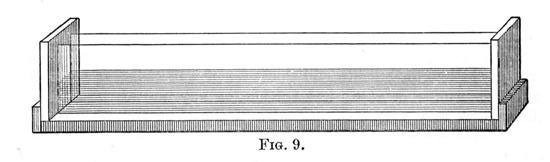
This is more than half filled with water, in which are immersed at different depths, balls of wax mixed with just so much iron filings, as will make them of the same specific gravity as water. Now alternately raise and depress one end of the box, so as to give rise to waves. The balls will describe closed curves in a vertical plane, the horizontal diameter of which will much exceed the vertical. If a deeper trough be taken, the difference between the horizontal and vertical diameters of these curves will become less; and in fact, in very deep water the two diameters become of the same length; that is, the closed curves become circles. It will be noticed also, that each particle of water describes its curve and returns to its original position, in the same time as the wave takes to move through its own length.
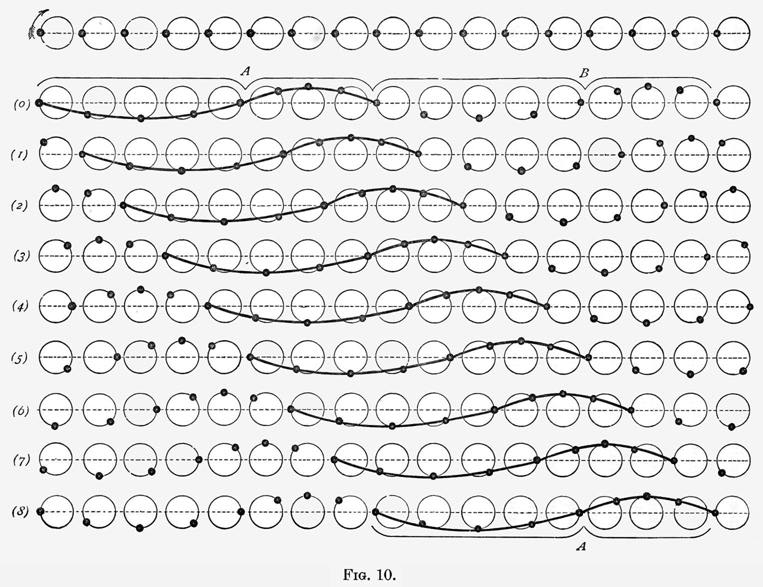
Bearing in mind these facts, we may plot out a water wave in the manner shown in figure 10. In the top row are 17 dots, representing 17 equidistant particles of water at rest, and the circles in which they are about to move, in the same direction as the hands of a clock. In (0), the position of each of these particles is given at the moment when they form parts of the two complete waves A and B, which are supposed to be passing from left to right; the 8th particle from the left has just passed through 1/8th of its journey, that is 1/8th of the whole circumference; the 7th particle has passed through 2/8=1/4; the 6th through 3/8; the 5th has just performed 1/2 its journey; the 4th, 5/8; the 3rd, 3/4; the 2nd, 7/8; and the first has just completed its course and regained its original position. In (1) each particle has moved through 1/8 more of its curve, and the wave has passed through a space equal to 1/8 of its length. In (2) each particle has moved through 1/8 more, and the wave has again advanced as before; and so on, in (3), (4), (5), (6), (7), and (8). Each particle in (8) has the same position as in (0), having made one complete journey; and the wave has advanced one wave length. Thus we see, as in the experiment with the trough, that each particle makes one complete journey in the same time as the wave takes to travel its own length.
Another variety of wave motion may be studied thus: Fill an india-rubber tube, about 12 feet long and 1/4 inch in diameter, with sand, and fasten one end to the ceiling of a room. Hold the other end in the hand, and jerk it sharply on one side. Notice the wave motion thus communicated to the tube, the wave consisting of two protuberances, one on each side of the position of the tube at rest; the one corresponding to the crest of the water wave, and the other to its trough. Let the uppermost row of dots in figure 11, represent 17 equidistant particles of the tube at rest; (0) gives the position of the particles when they form parts of two complete waves A and B; and (1) to (8) show their position at successive intervals of time, each equal to 1/8 of the time that it takes a particle to perform one complete vibration. By a careful inspection of this diagram, it will be seen that while each particle performs one complete vibration, the wave travels through a space equal to its own length.
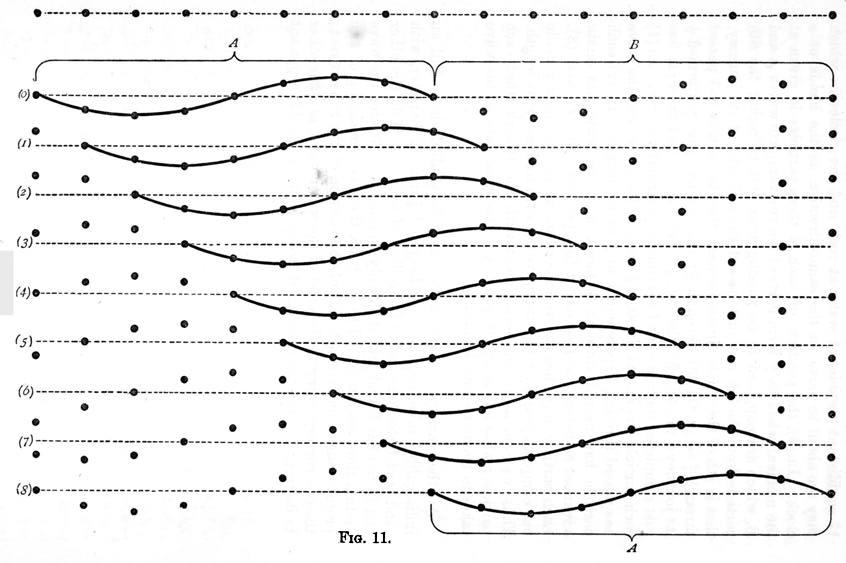
Taking the 1st particle in A, for example:- in (1), it has risen half way to its highest point; in (2), it has reached its highest point; in (3), it is descending again; in (4), it is passing downwards through its original position; in (5), it is still sinking; in (6), it has reached its lowest position; in (7), it is ascending again; in (8), it has reached its original position, having made one complete vibration. Now it is obvious from the figure, that during this time the wave A has passed through a space equal to its own length.
Let the curve in figure 12 represent the outline section of the wave A in figure 11. Through the deepest and highest points (d) and (c) of the protuberances, draw the dotted straight lines parallel to AB, the position of the tube when at rest. Through (d) draw (df) at right angles to AB; then as before (df) is the amplitude, of the wave. Now on comparing this with figure 11 it will be seen that this amplitude is the same thing as extent of vibration of each particle.

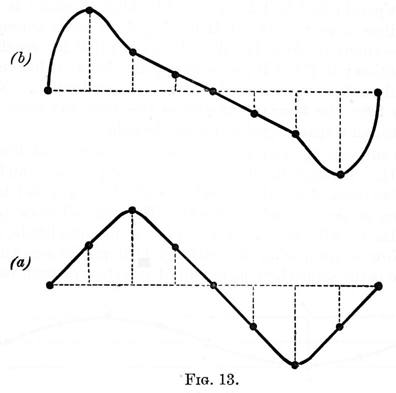
If we supose, that a particle takes a certain definite time, say one second, to perform its vibration, it is evident that the number of different modes in which it may get over its ground in this time is infinite. Thus it may move slowly at first, then quickly and again slowly; or it may start quickly, then slacken, again quicken, slacken again, and finish up quickly; and so on. In figure 13, two waves of equal length and amplitude are represented after the manner of figure 12. The extent and time of particle vibration being the same, they only differ in the mode of vibration. In (b) the particle at first moves more quickly than in (a); it then moves more slowly; and so on. Thus for example: supposing the time of a complete vibration to be one second, the particle in (a) reaches its highest position in one quarter, and its lowest, in three quarters of a second after the start; while in (b) the particle reaches the same points in 1/8, and 7/8 of a second, respectively. Now it is plain from the figure, that this difference in mode of particle vibration is accompanied by a difference in the form of the wave, and a little reflection will show that this must always be the case. We have thus seen how the length, amplitude, and form of a wave are respectively connected with the time, extent, and mode of particle vibration.
Having now made some acquaintance with wave motion in general, we may pass on to consider the particular case of the sound wave. The first point to which we must turn our attention, is the nature of the medium. Air, like every other gas, is supposed to be made up of almost infinitely small particles. These particles cannot be very closely packed together; in fact, they must be at considerable distances apart in proportion to their size, for several hundred volumes of air can be compressed into one volume. When air is thus compressed, the particles of which it consists, press against one another, and against the sides of the containing vessel in all directions; and that with a force which is the greater, the closer the particles are pressed together; in other words, the air is elastic. An ordinary popgun will illustrate this: a certain volume of air having been confined between the cork and the rammer of the gun, the latter is gradually pushed in; the air particles being thus crowded closer and closer together, exert an ever increasing pressure, until at length the weakest point, the cork, gives way.
Let A, figure 14 (1), represent a tuning-fork, and BC a long tube open at both ends. Suppose now, that the fork begins vibrating, its prongs first performing an outward journey. The air in BC will be condensed, but in consequence of the swiftness of the fork's motion, and the great elasticity of air, this condensation will be confined during the outward journey of the prongs, to a comparatively small portion of the tube BC: say to the portion (ab) figure 14 (2). The air in (ab), being now denser than that in advance of it will expand, acting on the air in (bC) as the tuning-fork acted upon it, thus causing a condensation in (bc) figure 14 (3), while the air in (ab) itself, overshooting the mark, as it were, becomes rarified, and effect which is increased by the simultaneous retreat of the prong A. Again, the air in (bc) figure 14 (3), being denser than that before and behind, expands both ways, forming condensations (cd) and (ab) figure 14 (4), in both directions; while in its place is formed the rarefaction (bc), the formation of the condensation (ab) being assisted by the outward journey of A. Next the air in (ab) and (cd) figure 14, being denser than that on either side, expands in both directions, forming the condensations (bc) and (de) figure 14 (5); rarefactions being formed in (ab) and (cd), the former assisted by the retreat of the prong A. By further repetitions of this process the sound waves (ac) and (ce) will be propagated along the tube.
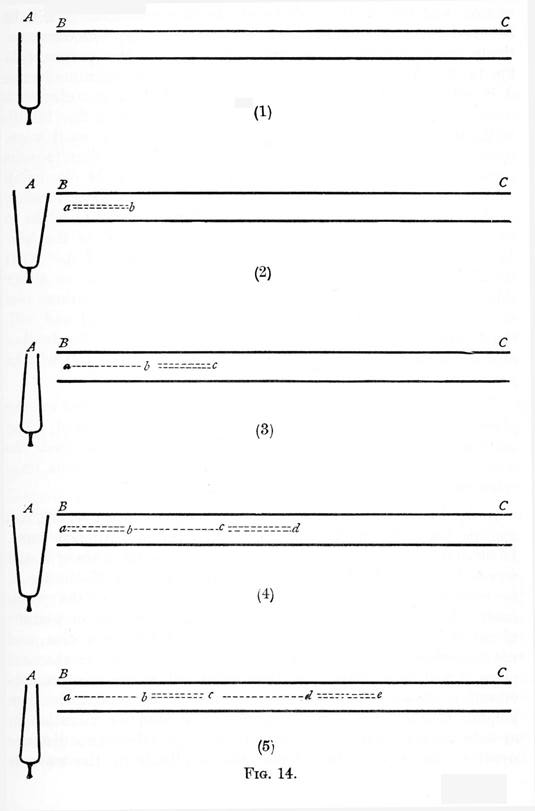
For the sake of simplicity, the motion has been supposed to take place in a tube. This restriction may now be removed. The movement of the air passing outward in every direction from the sounding body, the successive condensations and rarefactions form spherical concentric shells round it.
In figure 14 (5), (ac) and (ce) form two complete sound waves, (bc) and (de) being the condensed, and (ab) and (cd) the rarefied parts. In studying the motion of the particles of air forming these sound waves, it will be simplest to consider those adjoining the prong A, for their motion will necessarily be similar to that of the prong itself. The first point to notice is, that the direction of particle vibration in this case is the same as that of the wave motion, and not transversely to it as in the case of the sand tube. In the next place, it will be observed, that the tuning-fork makes one complete vibration while the wave passes through a space equal to its own length; that is, each particle executes one complete vibration in exactly the same time as the wave takes to pass through a distance equal to its own length. Again, the amplitude of the wave is evidently the distance through which the individual particles of air vibrate; that is, the extent of particle vibration. Further, it is plain that, the greater the swing of the prong A, the greater will be the degree of condensation and rarefaction in (ab); that is, the greater the extent of particle vibration, the greater will be the degree of rarefaction and condensation. Lastly, just as the particles in the case of the sand tube could perform their vibrations in an infinite number of modes, so the fork A, and therefore the air particles, may perform their vibrations in an endless variety of modes, giving rise to as many wave forms.
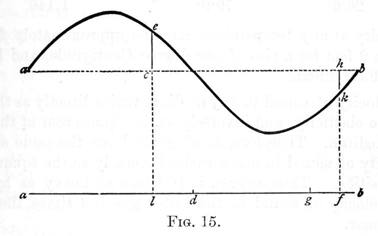
It is often convenient to represent a sound wave after the same manner as a water wave. Let figure 15 represent the section of a water wave, the dotted line being the surface of the water at rest. This may also represent a sound wave the length of which is (ab) distance above the dotted line representing extent of forward, and distance below extent of backward longitudinal vibration. For example, the air particles which are at the points l and f when at rest, would be at d and g, (ld = ce and hk = gf) in the state of things represented in the figure. The curve in the figure, related in this way to the wave of condensation and rarefaction, is termed its associated wave.
The velocity with which these sound waves travel is very great, compared with that of water waves. The method of determining it is very simple in principle. Two stations are chosen within sight of each other, the distance between them being accurately known. A gun is fired at one station, and an observer at the other counts the number of seconds that elapse between seeing the flash and hearing the sound. As light passes almost instantaneously over any terrestrial distance, the time that sound takes to travel over a given distance is thus known. Dividing this distance by the number of seconds, we determine the space through which sound travels per second. This is found to vary considerably with the temperature. At 0º (Centigrade) or 32º (Fahrenheit) the velocity of sound is 1,090 feet per second. M. Wertheim gives the following results at other temperatures:-
| Temperature. | Velocity | |
| Centigrade | Fahrenheit. | of Sound. |
| -.5º | 31.1º | 1,089 |
| 2.1º | 35.8º | 1,091 |
| 8.5º | 47.3º | 1,109 |
| 12º | 53.6º | 1,113 |
| 26.6º | 79.9º | 1,140 |
The velocity at any temperature may be approximately found by adding on 2 feet for a rise of one degree Centigrade, and 1 foot for a degree Fahrenheit.
The velocity of sound in any medium varies directly as the square root of the elasticity, and inversely as the square root of the density of that medium. Therefore, as all gases have the same elasticity, the velocity of sound in gases varies inversely as the square root of their densities. Thus oxygen is 16 times as heavy as hydrogen, and the velocity of sound in the latter gas is 4 times the velocity in the former.
Sound travels more quickly through water than through gases. Colladon and Sturm proved that the velocity of sound in water is 4,708 feet per second, at 8º Centigrade. Their experiments were conducted on the Lake of Geneva, on the opposite sides of which the observers were stationed in two boats. The sound was emitted under water by striking a bell with a hammer, and after travelling through a known distance was received by a long speaking tube, the larger orifice of which, a vibrating membrane, was sunk beneath the surface. The same movement which gave rise to the sound, also at the same instant ignited some gunpowder, and the number of seconds elapsing between the flash and the sound was determined by a chronometer.
In solids, the velocity of sound is usually greater than in liquids. It may be calculated from the formula
V = sqrt(E/ D)
when the elasticity E and density D of the solid are known.
The various experimental methods that have been employed for determining it, will be given later on. The following are some of the principal determinations made by Weitheim.
| Lead | 4,030 | feet per second at 20º C. |
| Gold | 5,717 | " " " " " |
| Silver | 8,553 | " " " " " |
| Copper | 11,666 | " " " " " |
| Platinum | 8,815 | " " " " " |
| Iron | 16,822 | " " " " " |
| Steel | 16,357 | " " " " " |
| Wood (along fibre)from | 10,000 to 15,000 | " " " |
| (across fibre) | 3,000 to 5,000 | " " " |
The superior conducting power of elastic solids may be illustrated by a variety of experiments. Thus, strike a tuning-fork and place the stem against the end of a rod of wood 12 or 15 feet long. So perfect is the transmission, that if a person applies his ear to the other end, the sound will appear to come from that part of the rod. A still better result is obtained by placing one end of the rod against a door panel, and applying the vibrating tuning fork to the other. Again, place a watch well between the teeth, without however touching them, and note the loudness of its tick. Now gently bite the watch, and observe how much more plainly it can be heard. In the first case, the vibrations pass through the air to the ears, in the second case, through the solid bones of the skull. This is the principle of the audiphone.
Summary.
(Audible) Sound cannot be transmitted through a vacuum.
The transmission of sound is a particular case of wave motion, of which, water waves and rope waves are other examples. The peculiar characteristic of a wave motion is, that the material particles through which the wave is passing, do not move onwards with the wave, but simply oscillate about their position of rest. In the rope wave, for example, the particles of the rope oscillate at right angles to the direction in which the wave is advancing; while, on the other hand, in the sound wave, the air particles oscillate in the same direction as the wave is moving.
Just as a water or rope wave consists of two parts, a crest and a trough, so a sound wave is made up of two portions, viz., a condensation and a rarefaction.
(The appearance of) A sound wave, like a water or rope wave, is determined by three elements, viz., its length, amplitude, and form. The length of a wave is the distance from any point in one wave to the corresponding point in the succeeding one; the amplitude is measured by the extent of vibration of its air particles; while the form is determined by the varying velocities of these particles as they perform their excursions.
The greater the amplitude (that is, the extent of particle vibration), the greater will be the degree of condensation and rarefaction.
In an associated sound wave, the direction of particle vibration is represented, for the sake of convenience, as being at right angles to its true direction.
The velocity of sound at the freezing point is 1,090 feet per second, and increases as the temperature rises.
The velocity of sound in water is 4,708 feet per second at 8º Centigrade.
The velocity of sound in elastic solids, such as iron and wood, is much greater than the above.
Footnote
(1) - What is meant here is "AUDIBLE" sound. Inaudible sound (compression wave) can indeed pass through a vacuum.
Return to Part 26 - Science of Sound, Vibration, Acoustics and Music
See Also
