Schauberger
"In the outbirth of water we have to differentiate between two different kinds. Namely water as a carrier-substance that contains predominantly negative potentialities (substances attuned to earth frequencies) or predominantly positive potentialities (substances attuned to air frequencies). The former are to be viewed as upwardly-impelling geospheric instrumentalities and the latter as downwardly-impelling atmospheric instrumentalities. The former refine and exalt the higher-grade constituents, i.e. they serve the build-up of levitative potencies. The latter serve to cleanse the atmosphere of suspended matter, which as threshold substances still possess too little self-weight and too high a quota of levitative essences and can neither rise nor fall. It is these threshold substances that can be transformed and exalted through cycloid-space-curve motion. From a practical point of view, this is only possible through their co-oscillation with their respective carrier-substances, be it air or water. This leads to a build-up of those substances incapable of further development, resulting in a renewed intensification of the differences in potential through the spacial separation of the difference-substances. The end result is an increased motive force. This explains the concept of perpetual motion in its most natural sense." [Viktor Schauberger, Implosion Magazine, No. 118, p. 8.] [The Energy Evolution - Harnessing Free Energy from Nature, THE NATURE OF WATER - ITS CONDUCTION AND USE FOR TRANSPORT]
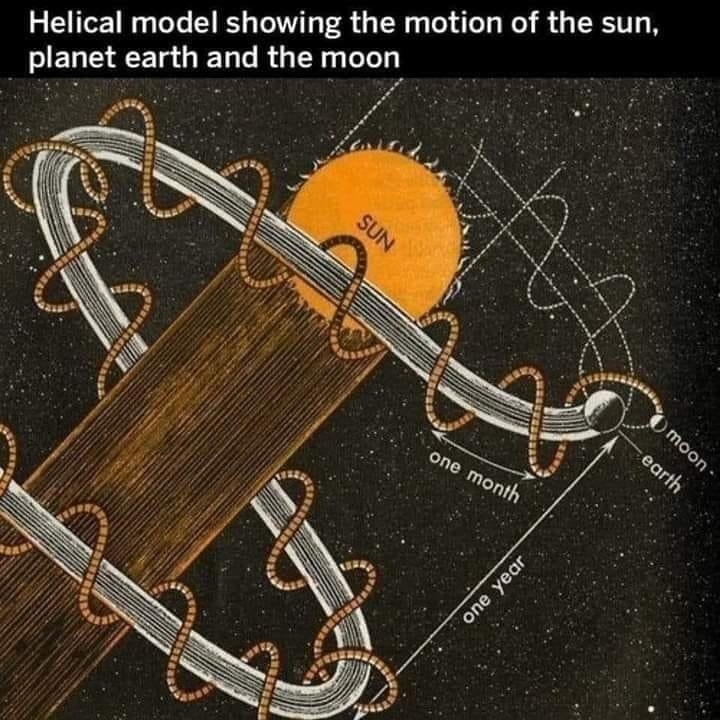
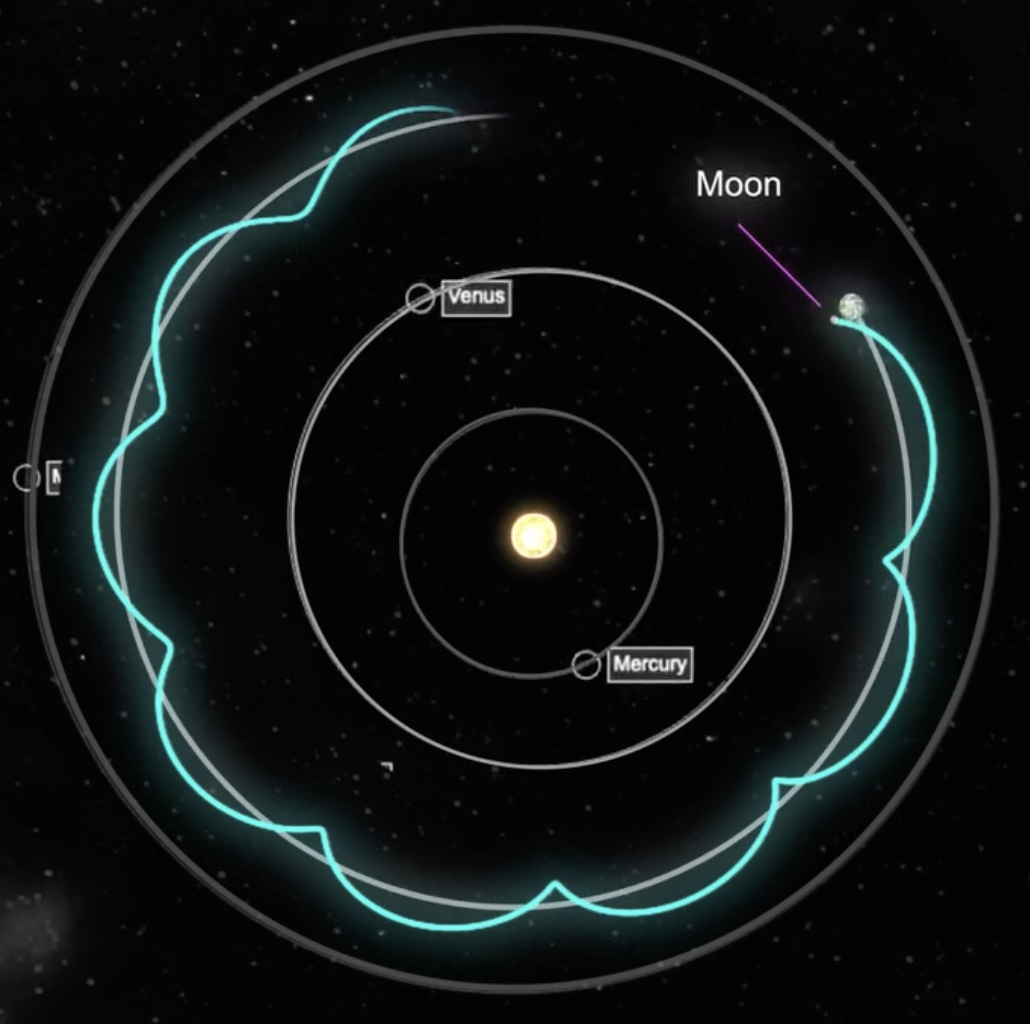
Examples of Cycloid Space Motions




Alex Isakov
Classical mechanics based on Newton's laws, as well as its evolution within the general theory of relativity, form the foundation of modern physics. These theories have provided humanity with effective tools for describing the motion of objects and the interaction of masses. However, upon deeper analysis, the question arises: have we really investigated inertial mass in its entirety? In particular, have we considered its true nature, taking into account all the components of motion? It turns out that what is commonly considered inertial mass is only an "incomplete" expression of it, which is due to the limitations of traditional physics in understanding angular velocity and its three-dimensional nature. Inertial mass in classical mechanics is defined through the resistance of an object to changing its state of motion under the action of a force. In most cases, the inertial mass is described in terms of the linear velocity, which is an emergent property that occurs at extreme values of the gyration radius R. When the gyration radius tends to infinity, the angular motion can be approximated by a linear motion, and in this case the inertial mass is expressed in terms of this linear motion.
However, this approach ignores the deep connection between angular and inertial mass. In traditional mechanics, we mainly study only one axis of rotation, and the inertial mass derived from this motion does not take into account all aspects of the dynamics.
The existing inertial mass arises from the one-dimensional angular velocity, which in turn is only a simplified manifestation of a more fundamental phenomenon - the three-dimensional angular velocity. When we ignore rotation about two of the three axes per cycle, we lose a significant part of the information that describes the true behavior of the inertial mass. This approach limits our understanding of mechanics because we simplify rotation to a one-dimensional case that does not tell the whole story.
Thus, traditional inertial mass is incomplete, and all of mechanics, the foundation of physics, relies on a limited understanding of linear velocity and 1D angular velocities and their effect on the mass of objects.
The full inertial mass can only be properly defined by taking into account the 3D angular velocity, which describes the rotation of an object around three axes at once during a cycle. When we consider the rotation of an object in its entirety, rather than just in one dimension, we find that inertial mass is not simply a result of the object's resistance to linear motion, but also a consequence of its complex interactions with space and time as it rotates.
Interestingly, the 1D angular velocity and the inertial mass derived from it are emergent phenomena that only occur when two of the three axes of rotation are ignored. This simplification inevitably leads to a distortion of the overall picture of mechanics, which in turn requires a revision of our ideas about the mass and motion of objects.
Modern physics and mechanics are built on the assumption that linear motion and the inertial mass associated with it are the main characteristics. However, if we take into account three-dimensional angular velocity, it becomes obvious that linear velocity is only a special case of more complex dynamics. This gap in understanding leads to the fact that the fundamental laws of mechanics are considered in an overly simplified form.
These simplifications are especially important in the context of complex systems, such as rotation in 6 degrees of freedom, where the total inertial mass of an object depends on its three-dimensional rotation. Studying this phenomenon can lead to new discoveries and a deeper understanding of how the motion of objects is related to their mass.
The study of the total inertial mass, including three-dimensional angular velocity, opens up new horizons for physics and mechanics. Current concepts of mass based on linear velocities and one-dimensional angular velocity are an incomplete description of the dynamics of objects. This gap in our knowledge must be filled in order to better understand the nature of mass and motion, which may lead to a fundamental revision of the foundations of mechanics and physics.
Further experiments are needed to confirm and develop the theory of full inertial mass, such as the study of the rotation of objects in three-dimensional systems with full freedom of movement. One possible step could be the use of prototypes of a power mechanical gyroscope - Gyro_6DoF, which demonstrate new physical effects associated with three-dimensional angular velocity and full inertial mass description. [Alex Isakov]
See Also
cycloid
cycloid motion
cycloid motive impulse
cycloid-space-curve
cycloid-space-curve motion
cycloid-space-curve system
cycloid-space-curve-motion
cycloid-spiral-space-curve
Hipparchus
motion
system of cycloid-space-curves
The Practical Application of Cycloid-Space-Curve-Motion arising from Processes of Cold Oxidation