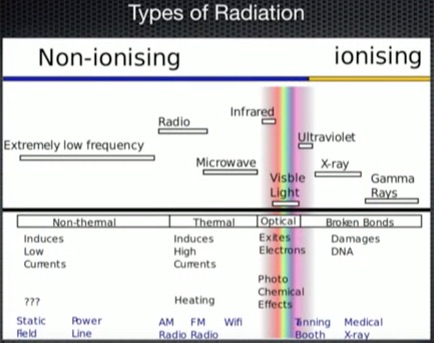
Radiation (click to enlarge)

The ionization energy of a chemical species, i.e. an atom or molecule, is the energy required to remove electrons from gaseous atoms or ions. The property is alternately still often called the ionization potential, measured in volts. In chemistry it often refers to one mole of a substance (molar ionization energy or enthalpy) and reported in kJ/mol. In atomic physics the ionization energy is typically measured in the unit electron volt (eV). Large atoms or molecules have a low ionization energy, while small molecules tend to have higher ionization energies.


The ionization energy is different for electrons of different atomic or molecular orbitals. More generally, the nth ionization energy is the energy required to strip off the nth electron after the first ‪n − 1‬ electrons have been removed. It is considered a measure of the tendency of an atom or ion to surrender an electron, or the strength of the electron binding; the greater the ionization energy, the more difficult it is to remove an electron. The ionization energy may be an indicator of the reactivity of an element. Elements with a low ionization energy tend to be reducing agents and form cations, which in turn combine with anions to form salts.

Electron binding energy (BE), more accurately, is the energy required to release an electron from its atomic or molecular orbital when adsorbed to a surface rather than a free atom. Binding energy values are normally reported as positive values with units of eV. The binding energies of 1s electrons are roughly proportional to (Z-1)² (Moseley's law). Wikipedia, Ionization Potential

Generally the (n+1)th ionization energy is larger than the nth ionization energy. Always, the next ionization energy involves removing an electron from an orbital closer to the nucleus. Electrons in the closer orbitals experience greater forces of electrostatic attraction; thus, their removal requires increasingly more energy. Ionization energy becomes greater up and to the right of the periodic table.

Some values for elements of the third period are given in the following table:

Element

First

Second

Third

Fourth

Fifth

Sixth

Seventh

Successive molar ionization energies in kJ/mol

(96.485 kJ/mol = 1 eV/particle)

Na	496	4,560
Mg	738	1,450	7,730
Al	577	1,816	2,881	11,600
Si	786	1,577	3,228	4,354	16,100
P	1,060	1,890	2,905	4,950	6,270	21,200
S	999.6	2,260	3,375	4,565	6,950	8,490	27,107
Cl	1,256	2,295	3,850	5,160	6,560	9,360	11,000
Ar	1,520	2,665	3,945	5,770	7,230	8,780	12,000

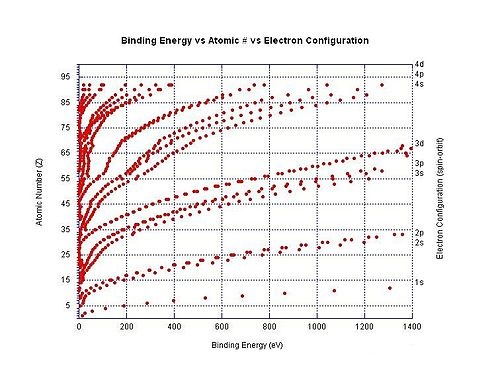
Large jumps in the successive molar ionization energies occur when passing noble gas configurations. For example, as can be seen in the table above, the first two molar ionization energies of magnesium (stripping the two 3s electrons from a magnesium atom) are much smaller than the third, which requires stripping off a 2p electron from the very stable neon configuration of Mg²⁺.

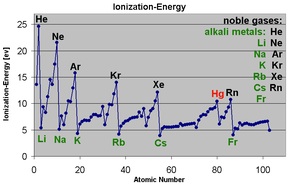
Ionization energy is also a periodic trend within the periodic table organization. Moving left to right within a period or upward within a group, the first ionization energy generally increases. As the atomic radius decreases, it becomes harder to remove an electron that is closer to a more positively charged nucleus. Ionization enthalpy increases from left to right in a period and decreases from top to bottom in a group. Wikipedia, Ionization Energy

Electrostatic explanation of Ionization Energy Atomic ionization energy can be predicted by an analysis using electrostatic potential and the Bohr model of the atom, as follows.

Consider an electron of charge -e and an atomic nucleus with charge +Ze, where Z is the number of protons in the nucleus. According to the Bohr model, if the electron were to approach and bind with the atom, it would come to rest at a certain radius a. The electrostatic potential V at distance a from the ionic nucleus, referenced to a point infinitely far away, is:

Since the electron is negatively charged, it is drawn inwards (syntropy) by this positive electrostatic potential. The energy required for the electron to "climb out" and leave (entropy) the atom is:

This analysis is incomplete, as it leaves the distance a as an unknown variable. It can be made more rigorous by assigning to each electron of every chemical element a characteristic distance, chosen so that this relation agrees with experimental data.

It is possible to expand this model considerably by taking a semi-classical approach, in which momentum is quantized. This approach works very well for the hydrogen atom, which only has one electron. The magnitude of the angular momentum for a circular orbit is:

The total energy of the atom is the sum of the kinetic and potential energies, that is:

Velocity can be eliminated from the kinetic energy term by setting the Coulomb attraction equal to the centripetal (syntropy) force, giving:

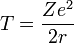
Solving the angular momentum for v and substituting this into the expression for kinetic energy, we have:

This establishes the dependence of the radius on n. That is:

Now the energy can be found in terms of Z, e, and r. Using the new value for the kinetic energy in the total energy equation above, it is found that:

At its smallest value, n is equal to 1 and r is the Bohr radius a_o. Now, the equation for the energy can be established in terms of the Bohr radius. Doing so gives the result:

See Also

---

Atomic Cluster Ionization Charge Electromagnetic Radiation Entropy Heaviside energy flow component ionization electric potential Penning Ionization Penning Mixture Photoionization Plasma Radiation Valence 12.32 - Ionization