Entropy has often been loosely associated with the amount of order, disorder, and/or chaos in a thermodynamic system. The traditional qualitative description of entropy is that it refers to changes in the status quo of the system and is a measure of "molecular disorder" and the amount of wasted energy in a dynamical energy transformation from one state or form to another. In this direction, several recent authors have derived exact entropy formulas to account for and measure disorder and order in atomic and molecular assemblies. One of the simpler entropy order / disorder formulas is that derived in 1984 by thermodynamic physicist Peter Landsberg, based on a combination of thermodynamics and information theory arguments. He argues that when constraints operate on a system, such that it is prevented from entering one or more of its possible or permitted states, as contrasted with its forbidden states, the measure of the total amount of 'disorder' in the system is given by the first equation. Similarly, the total amount of "order" in the system is given by the second equation.
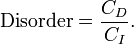
Disorder - Entropy (click to enlarge) |
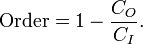
Order - Syntropy (click to enlarge) |
In which CD is the "disorder" capacity of the system, which is the entropy of the parts contained in the permitted ensemble, CI is the "information" capacity of the system, an expression similar to Shannon's channel capacity, and CO is the "order" capacity of the system. Wikipedia, Order and Disorder
See Also
Dynaspheric Force
Entropy
etheric seeks center
Figure 2.12.1 - Polarity or Duality
Gravism
Gravity
Law of Assimilation
Order
Ramsay - The Great Chord of Chords, the Three-in-One17
Rhythmic Balanced Interchange
Syntropy
Table of Cause and Effect Dualities
