To Question 2 and 3
[CONTINUED]
242
243
Without erring, it can furthermore be assumed that the Weissbach basic equation for frictional loss in pipes should also apply with outputs greater than 0.2 1/s, if at the inlet to the test pipes the formation of torsional motion could be prevented. Hence it is possible further to extend the parabola for the friction levels of the form h = 118 x q = 0.2 l/s. The differences in the ordinates between these parabolas and the q - h lines of the three test pipes, then represent the reduction in the amounts of friction normally applicable and as a consequence of this, can also be defined as the amounts of suction that the in-winding flowing motion of the water creates and which, as described above, form the basis for the calculation of the suction capacity.
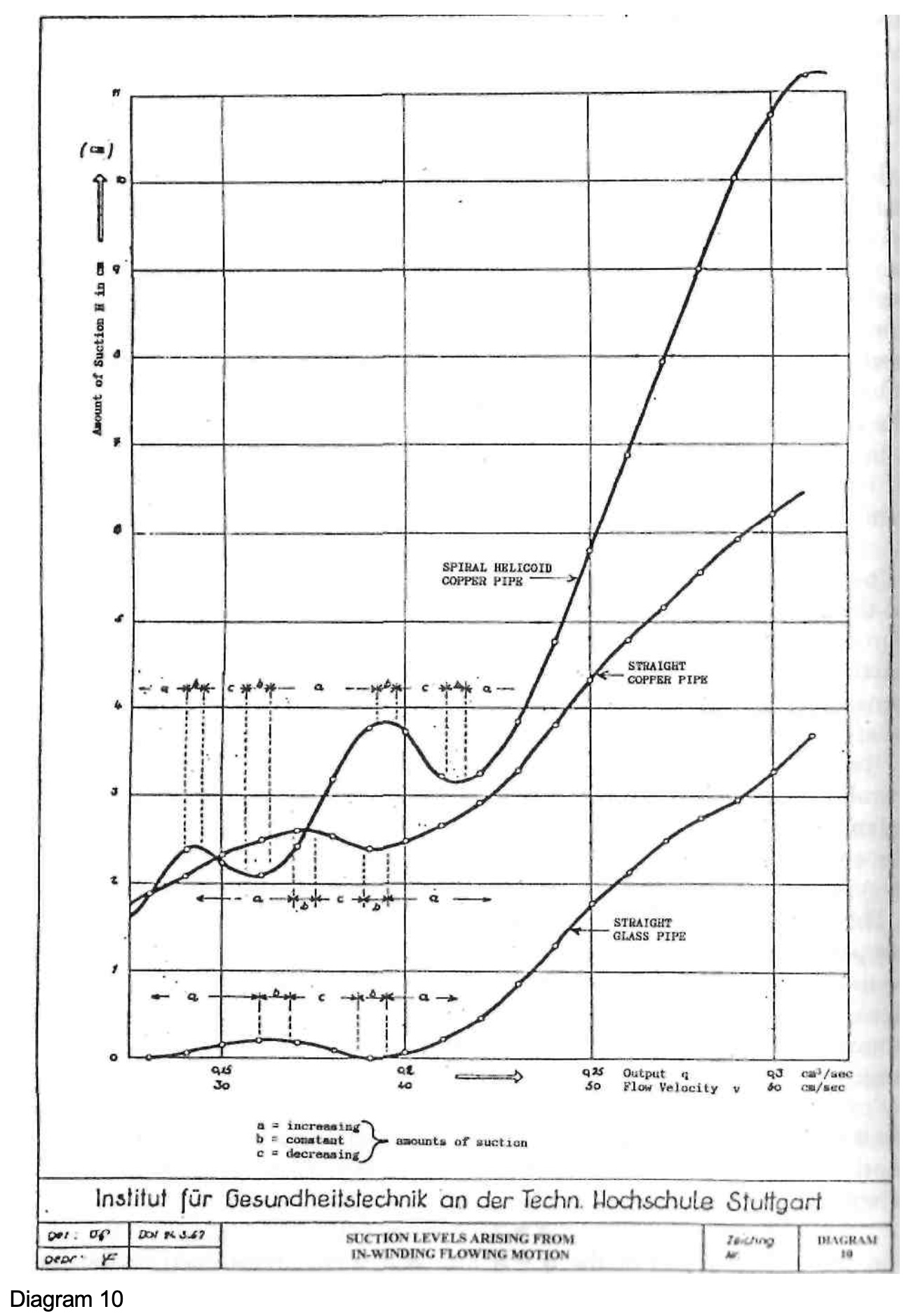
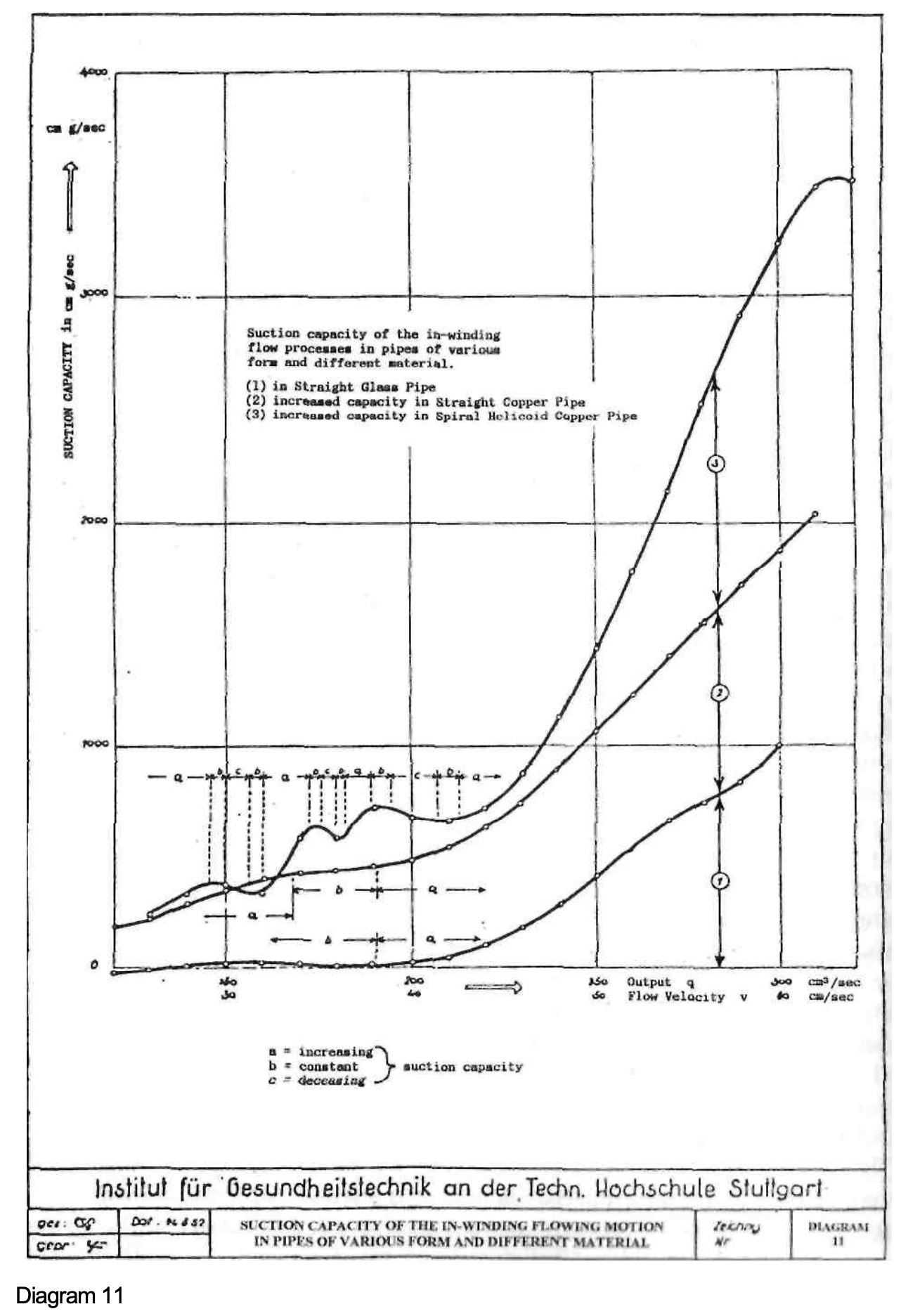
To illustrate these trains of thought, the amounts of suction based on the output were plotted in graph form in Diagram 10. With their aid the suction capacities A were determined, which in Diagram 11 were likewise plotted as q - A curves based on the output.
In the case of the glass pipe, the suction capacity constantly increases towards A = 850 cm g/s up to an output of q = 300 cm3/s. The copper pipe, however, under the same delivery volume, now develops a suction capacity of A = 1860 cm g/s. The material of the pipe has thus intensified the suction capacity exerted on the water by 1860 - 850 = 1010 cm g/s. With an output of 310 cm3/s the suction capacity of the spiral helicoid pipe reaches its maximum value in the examined area of measurement, where A = 310 x 11.1 = 3450 cm g/s. It is therefore 4.05 times as large as that of the glass pipe and 1.85 times larger than that of the straight copper pipe.
The course of the q - h and q - A lines in respect of the three test pipes shown in Diagrams 10 and 11 makes the rhythmical fluctuation of increasing, constant and decreasing amounts of suction with increasing output clearly apparent.
In the zones of increasing amounts of suction and suction capacity, the amount of suction arising from the multiple in-winding flowing motion of the water is always greater than the amount of friction to which, according to the Weissbach principle, the normal turbulent flow processes in pipes would give rise. The interpretation and evaluation of the observations selected above hence also permit the hypothetical conclusion, that the synchronisation of the kinetic energy of the flowing water generates more energy due to the spiralling and twisting of the pipes than is required to overcome the frictional losses obtaining. A constantly increasing acceleration of the motion of the water would therefore have to occur.
This acceleration, however, cannot assume unlimited proportions, since the zones of increasing amounts of suction and suction capacity are repeatedly interrupted by those of constant and decreasing suction capacity. These interruptions only occur, when the optimum synchronisation of all the flow processes is exceeded, leading to the accentuation of the dynamic translatory
244
245
component at the expense of the rotational and oscillatory motions, whereby an asynchronous combined action of the various superimposed kinetic processes comes about. The course of the curves demonstrates that in the investigated area of measurement, these consist of relatively long sections of increasing suction capacity, interrupted by shorter sections of constant and decreasing suction capacity. In the areas of constant amounts of suction and suction capacity, the gain in energy arising from the in-winding flowing motion of the water - corresponding to the observation in the glass pipe - is just as large as the consumption of energy, which the normal turbulent flow would cause. The gain in energy however, as in the case of the copper pipe, can also be of a greater constant amount than the normal consumption of energy in turbulent flow processes.
In the zones of decreasing amounts of suction and suction capacity, the kinetic energy of the flowing and rotating water is not synchronised with its oscillating motion.[1] Through this the turbulence of the currents is intensified to the extent that the consumption of energy required to convey the water in the pipes is much greater than the energy gain arising from the in-winding motion of the water.
Therefore the fact cannot be disregarded, that the representation of the observations in the above form may not reflect reality. It was employed first and foremost in order to obtain an initial overview of the magnitude of the forces capable of giving rise to the phenomenon of the in-winding flowing motion. It must be left to further experiments to understand their magnitude, form and effect more precisely. Since their existence has now become known and their conscious technical application lies within the bounds of possibility, they will be awarded a revolutionising importance in the areas of the handling and conveyance of liquid and gaseous media.
Since the courses of the q - h, q - H and q - A lines permit the recognition of the superiority of the spiral helicoid pipe vis-a-vis the straight copper pipe and the inferiority of the glass pipe with respect to the latter, Questions 2 and 3 can be collectively answered as follows:
The form and the material of the pipes are of decisive importance for the formation of the in-winding flow motion and the suction capacity and amount of suction generated by it.
[1] Same as Keely's negatization to coincident action.
Return to The Energy Evolution - Harnessing Free Energy from Nature
See Also
coincident action - negatization to